Contents

Lezione 12: fit di distribuzioni binnate con ROOT

Lezione 12: fit di distribuzioni binnate con ROOT

12.1 Introduzione

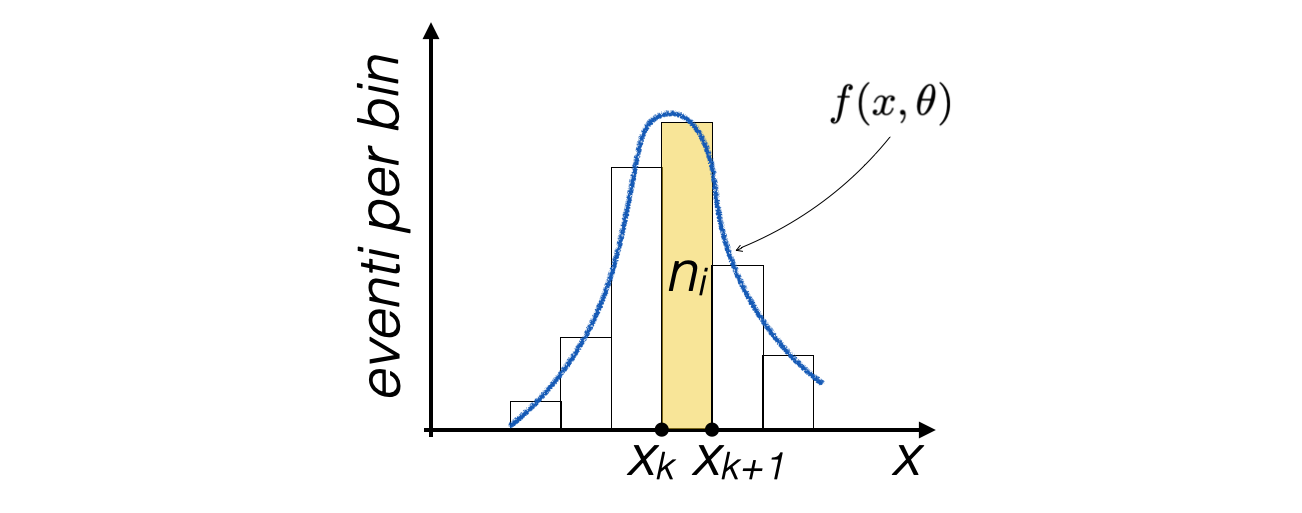
  • I metodi dei minimi quadrati e della massima verosimiglianza possono essere applicati anche al caso di istogrammi, cioè di distribuzioni binnate, dove si voglia fittare una funzione alla distribuzione dei conteggi nei bin: histo

  • In questo caso, il contenuto di ogni bin è un numero di eventi \(n_i\)

  • Se il numero di bin e il numero medio di eventi in ciascuno di essi non è piccolo, si può assumere che la variabile casuale \(n_i\) segua una statistica di Poisson

    \[ \mathcal{P}(n,\mu)=\frac{e^{-\mu}\mu^n}{n!} \]

linea

12.1.1 L’applicazione del metodo dei minimi quadrati

  • Nel caso dei minimi quadrati, la funzione Q2(θ) è solitamente la seguente (formulazione di Neyman):

    \[ Q^2(\theta) = \sum_{i=1}^N\left(\frac{n_i-f(x_i,\theta)}{\sqrt{n_i}}\right)^2 \]

  • Il valore di \(y_i\) della lezione scorsa è costituito da \(\mathbf{n_i}\)

  • L’incertezza su \(\mathbf{n_i}\) è data dalla sua radice quadrata, secondo la statistica di Poisson

  • Il valore di \(x_i\) è il centro del bin corrispondente

  • Il numero di bin dell’istogramma è \(N\)

linea

12.1.2 L’applicazione del metodo della massima verosimiglianza

  • Nel caso della massima verosimiglianza, si assume che in ogni bin i conteggi seguano una distribuzione di probabilità Poissoniana con valore atteso \(\mu = f(x_i, \theta)\):

    \[ \mathcal{L}(\theta) = \prod_{i=1}^N \frac{e^{-f(x_i,\theta)}f(x_i,\theta)^{n_i}}{n_i!} \]

linea

12.1.3 La scelta fra le due tecniche

  • Nel caso di pochi conteggi presenti nei bin,

    • bin senza conteggi non contribuiscono al fit nel caso dei minimi quadrati, nonostante l’assenza di eventi sia un’informazione importante

    • consigliato utilizzare il metodo della massima verosimiglianza

  • Nel caso di molti conteggi presenti nei bin, i due metodi sono equivalenti e spesso il metodo dei minimi quadrati è computazionalmente più semplice

linea

12.2 Un esercizio di regressione

  • Supponiamo di raccogliere eventi lungo una variabile x e di voler determinare i parametri della distribuzione di probabilità della variabile

  • Assumiamo che questo modello abbia una forma data da una distribuzione di fondo esponenziale sommata ad una di segnale gaussiana:

    \[\begin{split} \begin{align} f(x) &= \exp(x;\theta_0,\theta_1) + \mathcal{G}(x;\theta_2,\theta_3,\theta_4)\\ &= e^{(\theta_0+\theta_1 x)} + \theta_2\cdot e^{-\frac{1}{2}\left(\frac{x-\theta_3}{\theta_4}\right)^2} \end{align} \end{split}\]

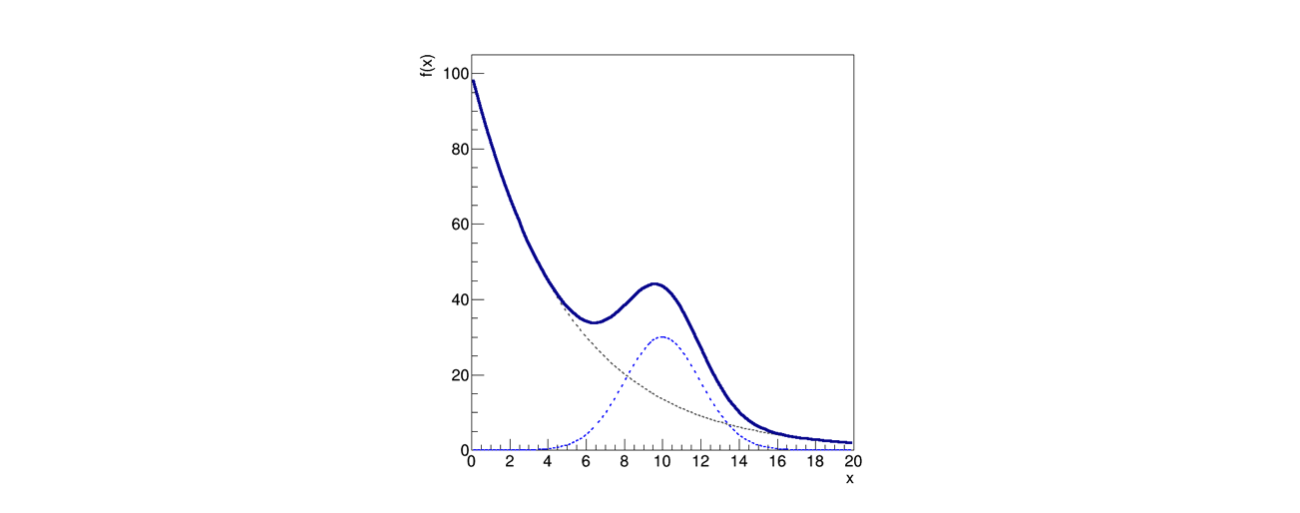
  • Graficamente, il modello ha un andamento decrescente che risale quando il termine Gaussiano diventa importante, come mostrato in figura: modello

    • la linea continua mostra il modello totale

    • mentre le due linee tratteggiate mostrano i due termini della somma, che si possono pensare come un picco di segnale sovrapposto ad un fondo lentamente decrescente

      (esempio 12.0)

linea

12.2.1 La lettura dei dati

  • Supponiamo di aver raccolto 10,000 eventi, che si trovano salvati nel file dati.txt

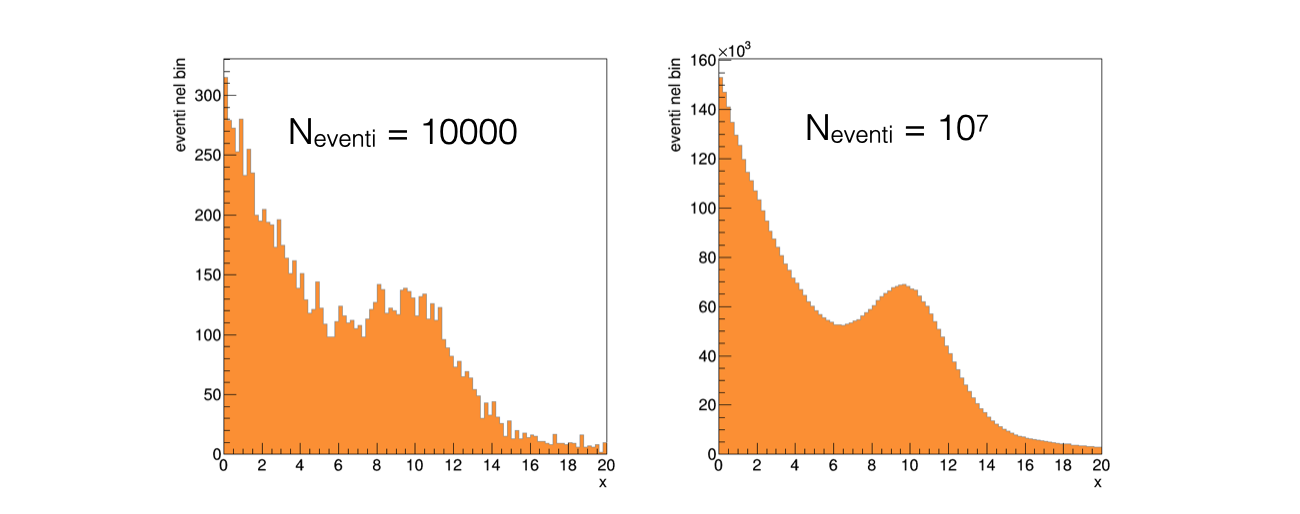
  • Quando si visualizzano gli eventi in un istogramma, siccome si tratta di un esperimento di conteggio il contenuto di ogni bin fluttua in maniera stocastica: distribuzioni

    • Nel caso di 10,000 eventi le fluttuazioni relative sono molto più accentuate del caso con 10,000,000 di eventi, come ci si aspetta

    (esempio 12.1)

linea

12.2.2 La determinazione dei parametri

  • Per determinare i parametri θ si utilizza tipicamente il metodo dei minimi quadrati o della massima verosimiglianza

  • In entrambi i casi, bisogna trovare l’estremante di una funzione

    • con molti parametri

    • in presenza di fluttuazioni statistiche

  • In questa lezione si ricorrerà agli algoritmi disponibili in ROOT per poter trattare un problema sofisticato

linea

12.2.3 Il fit di un istogramma in ROOT

  • Per poter effettuare il fit, è necessario definire il modello funzionale nel linguaggio di ROOT

  • Una funzione si rappresenta con un oggetto di tipo TF1:

    TF1 segnale ("segnale", "gaus(0)", 0., 20.) ;
segnale.SetParameter (0, p2) ;
segnale.SetParameter (1, p3) ;
segnale.SetParameter (2, p4) ;

    • In questo caso, la funzione sfrutta l’implementazione interna di ROOT della Gaussiana

    • La funzione è definita sull’intervallo 0., 20.

    • La gaus ha tre parametri, perché per fittare un istogramma non normalizzato anche l’integrale della funzione è un parametro libero

    • L’indice del primo parametro è 0, come indicato fra parentesi in gaus(0)

    • Il metodo TF1::SetParameter permette di assegnare valori ai parametri

linea

12.2.4 Il fondo ed il modello completo

  • Analogamente, la distribuzione di probabilità del rumore di fondo è:

    TF1 fondo ("fondo", "expo(0)", 0., 20.) ;

  • Il modello totale, indipendente dai primi due, è:

    TF1 model ("model", "expo(0) + gaus(2)", 0., 20.) ;

    • In questo caso, l’indice dei parametri della Gaussiana inizia da 2

linea

12.2.5 Il fit del modello ai dati

  • L’operazione di fit viene effettuata con il seguente comando, che invoca il metodo dei minimi quadrati:

    TFitResultPtr fit_result = h_eventi.Fit ("model", "S") ;

  • Dopo il fit, la funzione con nome "model" ha i propri parametri adattati all’istogramma

  • L’oggetto TFitResultPtr contiene i risultati del fit

  • Difficilmente il fit ha successo autonomamente, perché a causa del gran numero di parametri θ e delle fluttuazioni stocastiche del contenuto dei bin il programma non riesce a trovare il minimo giusto della funzione \(Q^2\)

linea

12.2.6 Come aiutare ROOT a trovare il minimo giusto

  • Per facilitare il fit, è molto efficace dare a ROOT un punto di partenza non distante dal risultato finale, basandosi sulla conoscenza del problema:

    • I parametri \(\theta_0\) e \(\theta_2\) sono l’integrale delle due funzioni di segale e fondo, quindi sono legati all’integrale dell’istogramma:

      double N_bkg = v_eventi.size () / 2. ;
double p0 = log (N_bkg) ;             // eventi di fondo
double p2 = v_eventi.size () / 2. ;   // eventi di segnale
model.SetParameter (0, p0) ;
model.SetParameter (1, p1) ;

    • L’esponenziale è sicuramente decrescente:

      double p1 = -0.5 ;                    // pendenza del fondo

    • Il massimo della Gaussiana si trova circa a metà dell’intervallo:

      double p3 = 0.5 * (max - min) ;       // media del segnale

    • La larghezza della Gaussiana è per un certo livello correlata alla sigma dell’istogramma:

      double p4 = h_eventi.GetRMS () ;      // sigma del segnale

linea

12.2.7 Come maneggiare meno parametri alla volta

  • Talvolta anche partendo da valori ragionevoli dei parametri il fit non converge all’estremante cercato

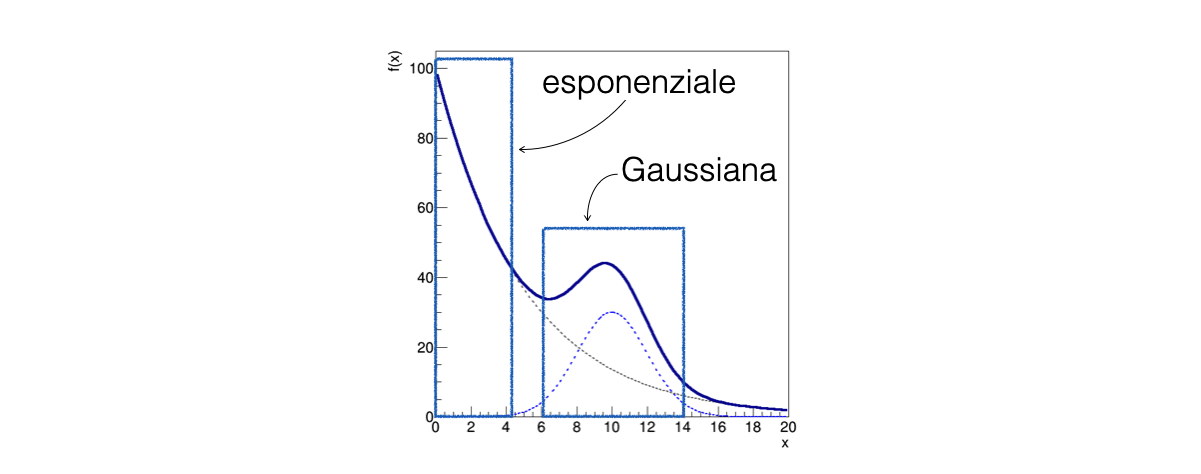
  • In questo caso, può essere d’aiuto identificare una regione dello spettro di x dove soltanto un sottoinsieme dei parametri è rilevante modello_regioni

linea

12.2.8 I parametri dell’esponenziale dalla regione esponenziale

  • Un fit parziale soltanto sull’intervallo 0., 4. con la distribuzione di probabilità del solo fondo permette di calcolare una stima preliminare di \(\theta_0\) e \(\theta_1\)

    TF1 fondo ("fondo", "expo(0)", 0., 20.) ;
fondo.SetParameter (0, p0) ;
fondo.SetParameter (1, p1) ;
h_eventi.Fit ("fondo", "Q", "", 0., 4.) ;

    • L’opzione "Q" fa in modo che nulla venga scritto a schermo

  • Un fit parziale soltanto sull’intervallo 7., 14. con la distribuzione di probabilità del solo segnale permette di calcolare una stima preliminare di \(\theta_3\) e \(\theta_4\)

    TF1 segnale ("segnale", "gaus(0)", 0., 20.) ;
segnale.SetParameter (0, p2) ;
segnale.SetParameter (1, p3) ;
segnale.SetParameter (2, p4) ;
h_eventi.Fit ("segnale", "Q", "", 7., 14.) ;

linea

12.2.9 Il fit finale

  • Dopo aver impostato i parametri iniziali della funzione "model" con i valori ricavati in precedenza, si effettua il fit finale:

    model.SetParameter (0, fondo.GetParameter (0)) ;
model.SetParameter (1, fondo.GetParameter (1)) ;
model.SetParameter (2, segnale.GetParameter (0)) ;
model.SetParameter (3, segnale.GetParameter (1)) ;
model.SetParameter (4, segnale.GetParameter (2)) ;    

TFitResultPtr fit_result = h_eventi.Fit ("model", "S") ;

    • L’opzione "S" garantisce che il risultato del fit venga salvato e sia accessibile tramite l’oggetto fit_result

linea

12.3 L’analisi del risultato della regressione

  • La funzione di fit viene automaticamente aggiunta alla proprietà del TH1F e visualizzata quando viene invocato il metodo TH1F::Draw: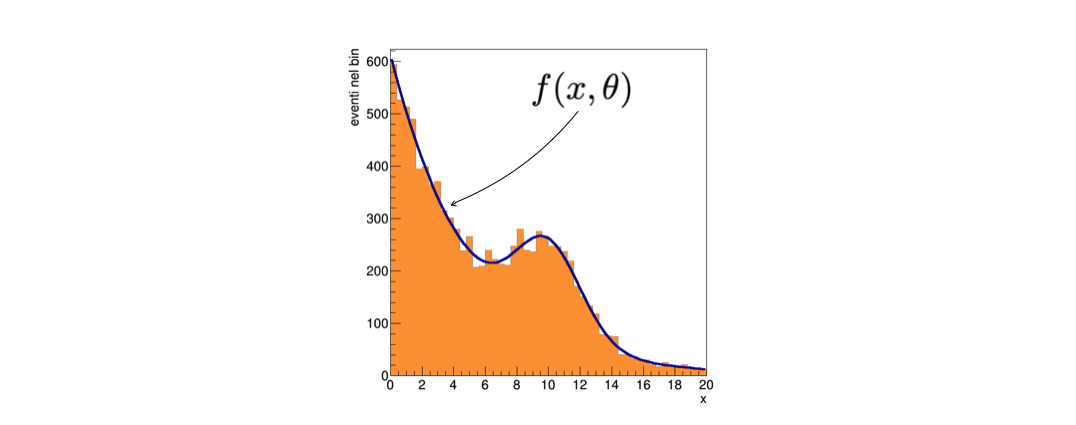 fit_result

linea

12.3.1 La stampa a schermo del risultato

  • L’output a schermo del fit ha la forma seguente:

     FCN=43.2314 FROM MIGRAD    STATUS=CONVERGED     136 CALLS         137 TOTAL
                     EDM=1.23203e-07    STRATEGY= 1  ERROR MATRIX UNCERTAINTY   5.6 per cent
  EXT PARAMETER                                   STEP         FIRST   
  NO.   NAME      VALUE            ERROR          SIZE      DERIVATIVE
   1  p0           6.42014e+00   1.80871e-02   1.13175e-05   2.97351e-03
   2  p1          -1.96538e-01   4.53819e-03   5.31592e-06   1.27147e-01
   3  p2           1.76316e+02   6.42286e+00   1.74578e-02  -3.17192e-05
   4  p3           9.97488e+00   7.97750e-02  -1.12275e-04   1.19307e-03
   5  p4           2.08229e+00   8.35661e-02  -1.64878e-04   1.22967e-04

    • In questo caso, l’algoritmo di minimizzazione utilizzato è MIGRAD

    • L’algoritmo ha avuto successo: STATUS=CONVERGED

    • I valori dei singoli parametri e della loro incertezza sono riportati a schermo

  • Le singole informazioni si possono recuperare anche dentro il codice sorgente

linea

12.3.2 La convergenza del fit

  • Per conoscere il successo dell’algoritmo numerico, si utilizza il metodo TFitResult::IsValid (), che deve essere true in caso di successo, oppure il metodo TFitResult::Status (), che deve essere 0 in caso di successo

    cout << "primo feedback sul risultato del fit: " << fit_result->IsValid () << endl ;
cout << "primo feedback sul risultato del fit: " << fit_result->Status () << endl ;

    • La classe TFitResultPtr si comporta come un puntatore ad oggetti di tipo TFitResult

linea

12.3.3 Il valore dei parametri e la loro incertezza

  • Il valore dei parametri e della loro incertezza possono essere ottenuti dalla funzione di fit:

    cout.precision (3) ; // stampa soltanto tre cifre significative
cout << "eventi di fondo:    " << exp (model.GetParameter (0)) << "\t+- "
                               << model.GetParError (0) * exp (model.GetParameter (0)) << endl ;
cout << "pendenza del fondo: " << model.GetParameter (1) << "\t+- " << model.GetParError (1) << endl ;
cout << "eventi di segnale:  " << model.GetParameter (2) << "\t+- " << model.GetParError (2) << endl ;
cout << "media del segnale:  " << model.GetParameter (3) << "\t+- " << model.GetParError (3) << endl ;
cout << "sigma del segnale:  " << model.GetParameter (4) << "\t+- " << model.GetParError (4) << endl ;

linea

12.3.4 La bontà del fit

  • Nel caso in cui la distribuzione di densità di probabilità dei singoli \(n_i\) sia Gaussiana, \(Q^2_{\text{min}}\) segue la distribuzione del \(\chi^2\) con \(N-k\) gradi di libertà, con \(N\) il numero di bin fittati e \(k\) il numero di parametri determinati

  • È necessario che per ogni bin ci siano abbastanza eventi, per cui la distribuzione di Poisson sia simile ad una Gaussiana

  • In queste condizioni si può utilizzare il test del \(\chi^2\) per determinare la bontà del fit calcolando la probabilità che il risultato possa essere peggiore di quello ottenuto, integrando la distribuzione di \(\chi^2(N-k)\) da \(Q^2_{\text{min}}\) all’infinito. L’integrale si può ottenere in due modi:

    cout << "probabilità associata a Q2: " << model.GetProb () << endl ;
cout << "probabilità associata a Q2: " << fit_result->Prob () << endl ;

    • Più alto è l’integrale, più si è fiduciosi del fit

  • Si possono anche ottenere il valore di \(Q^2_{\text{min}}\) e del numero di gradi di libertà dalla variabile fit_result

    cout << "Valore di Q2: " << fit_result->Chi2 () << endl ;
cout << "Numero di gradi di libertà: " << fit_result->Ndf () << endl ;

linea

12.3.5 La matrice di covarianza dei parametri risultanti

  • La matrice di covarianza e di correlazione dei parametri risultati può essere stampata a schermo:

    fit_result->PrintCovMatrix (cout) ;

  • I singoli valori sono accessibili tramite un oggetto di tipo TMatrixDSym (una matrice simmetrica), che si ottiene sempre dall’oggetto fit_result:

    TMatrixDSym cov = fit_result->GetCovarianceMatrix () ;
// or TMatrixDSym cov = r->GetCorrelationMatrix();
for (int i = 0; i < cov.GetNrows () ; ++i)
  {
    for (int j = 0; j < cov.GetNcols () ; ++j)
      {
        cout << cov(i,j) << "\t" ;
      }
    cout << "\n";
  }
    (esempio 12.2)

linea

12.4 Minimi quadrati (MQ) e massima verosimiglianza (ML)

  • Il metodo dei minimi quadrati (MQ) e quello della massima verosimiglianza (ML, da maximum likelihood) sono stimatori dei parametri di un modello, a partire dai dati

  • I due stimatori godono di proprietà diverse ed hanno comportamenti differenti: pur utilizzando gli stessi dati, possono produrre risultati differenti

linea

12.4.1 Il fit di massima verosimiglianza in ROOT

  • Per svolgere un fit con il metodo della massima verosimiglianza, è sufficiente aggiungere l’opzione "L" all’istruzione di fit:

    // fit con i minimi quadrati
TFitResultPtr fit_result_MQ = h_eventi.Fit ("model", "SQ+") ;
// fit con la massima verosimiglianza
TFitResultPtr fit_result_ML = h_eventi.Fit ("model", "SLQ+") ;

  • L’oggetto di tipo TFitResultPtr prodotto nei due casi contiene le stesse variabili

    • Anche nel caso della massima verosimiglianza viene calcolato il valore di Q2min, per poter effettuare il test del \(\chi^2\)

      (esempio 12.4)

linea

12.4.2 Il confronto fra due risultati

  • Per un grande numero di eventi, i due stimatori si equivalgono

  • Per un numero ridotto di eventi, invece, lo stimatore di massima verosimiglianza considera propriamente anche i bin vuoti e attribuisce più importanza alle code delle distribuzioni
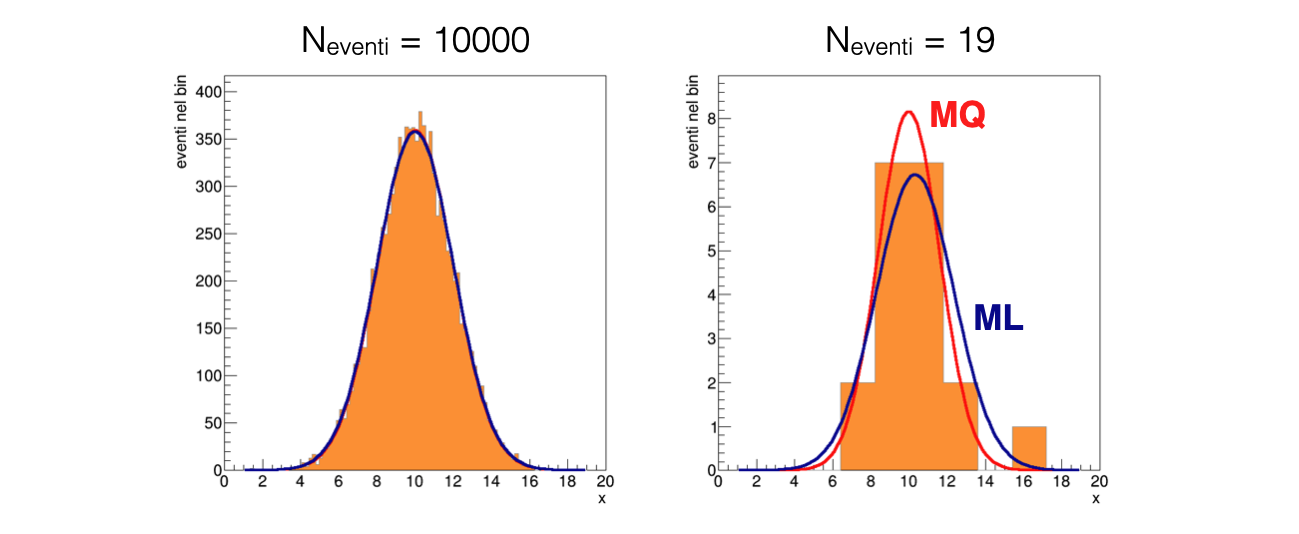
    ML_vs_MQ

(esempio 12.5)

linea

12.4.3 Il disegno del risultato

  • L’opzione "+" nell’istruzione di fit impone a ROOT di salvare nell’oggetto TH1F una copia della funzione utilizzata pr effettuare il fit.

  • La funzione può essere recuperata con il metodo TH1F::GetFunction

    // fit con i minimi quadrati
TFitResultPtr fit_result_MQ = h_eventi.Fit ("model", "SQ+") ;
h_eventi.GetFunction ("model")->SetLineColor (kRed) ;

    • Siccome il modello è sempre il medesimo, TH1F::GetFunction può generare ambiguità; la lista delle funzioni associate ad un TH1F si può ottenere anche con il metodo TH1F::GetListOfFunctions()

linea

12.5 Sulla scelta del binning

  • Siccome la scelta del binning determina il numero ed il valore dei punti \(n_i\), essa ha impatto sul risultato del fit

  • Scegliere bin con dimensioni molto piccole (e quindi un gran numero di bin)

    • rende distorto il metodo dei minimi quadrati, per via della possibile presenza di bin vuoti

    • rende inaffidabile il test del \(\chi^2\) per la bontà del fit

  • Scegliere bin con dimensioni molto grandi riduce la sensibilità degli stimatori, perché peggiora la risoluzione con la quale gli stimatori hanno accesso ai dati

    • Si può utilizzare il test del \(\chi^2\) per determinare la scelta del binning ottimale

linea

12.6 ESEMPI

  • Gli esercizi relativi alla lezione si trovano qui

12.7 ESERCIZI

  • Gli esercizi relativi alla lezione si trovano qui

previous

Soluzioni: Lezione 11

next

Esempi: Lezione 12