.md .pdf

Contents

Lezione 6: zeri ed estremanti di funzioni

Indice

• 6.1 alla ricerca degli zeri di una funzione

  • 6.1.1 il metodo della bisezione

  • 6.1.2 una implementazione dell’algoritmo di bisezione

  • 6.1.3 una implementazione dell’algoritmo di bisezione in modo ricorsivo

• 6.2 la ricerca di estremanti: il metodo della sezione aurea

  • 6.2.1 il criterio di restringimento

  • 6.2.2 l’ottimizzazione della scelta dei punti

• 6.3 mettere tutto insieme

• 6.4 il disegno di funzioni e punti in ROOT

• 6.5 ESEMPI

• 6.6 ESERCIZI

6.1 alla ricerca degli zeri di una funzione

• Esistono tecniche numeriche per trovare gli zeri di una funzione

Ipotesi semplici

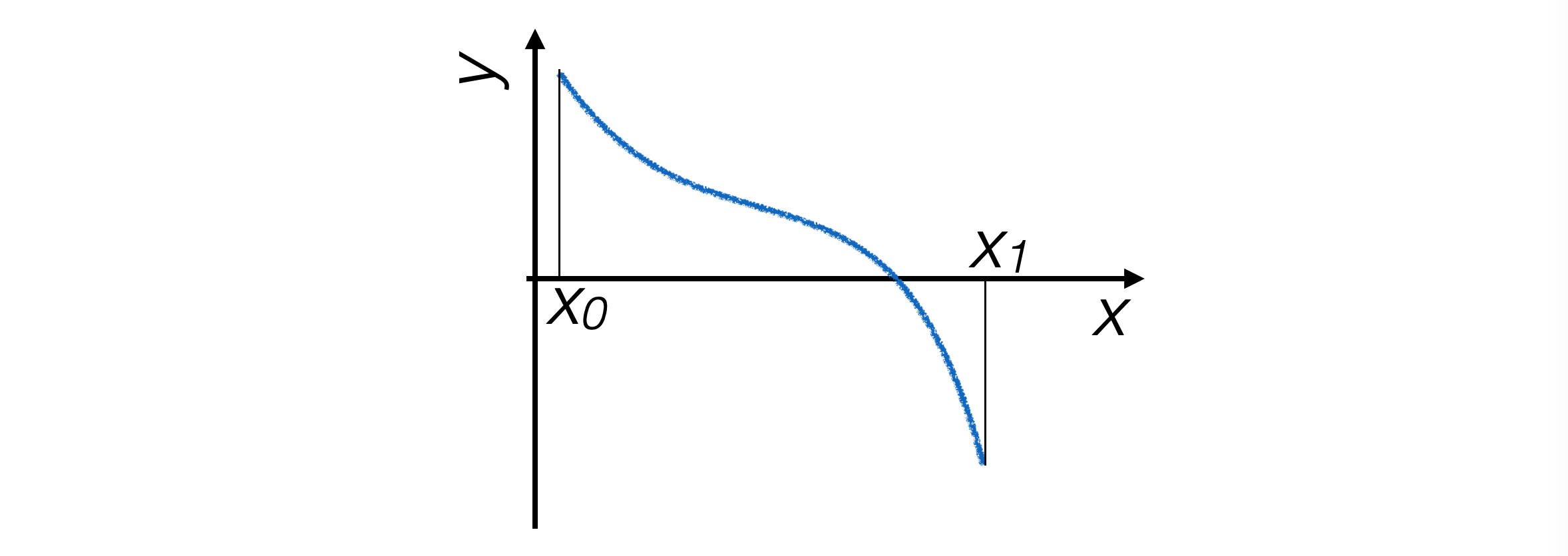
• Funzione g(x) continua definita su un intervallo compatto e connesso [x₀, x₁]

• Agli estremi dell’intervallo, i valori della funzione hanno segno opposto

• La funzione ha un solo zero nell’intervallo

6.1.1 il metodo della bisezione

• Il programma non vede la funzione nella sua interezza, quindi l’unico modo che ha per determinare dove sia lo zero è stimare la funzione in singoli punti

• Date le ipotesi iniziali, lo zero della funzione si trova sicuramente fra due punti tali per cui la funzione assume valore con segno opposto fra questi due punti

• La tecnica della bisezione restringe iterativamente questo intervallo
  fino a che non diventa più piccolo di una risoluzione fissata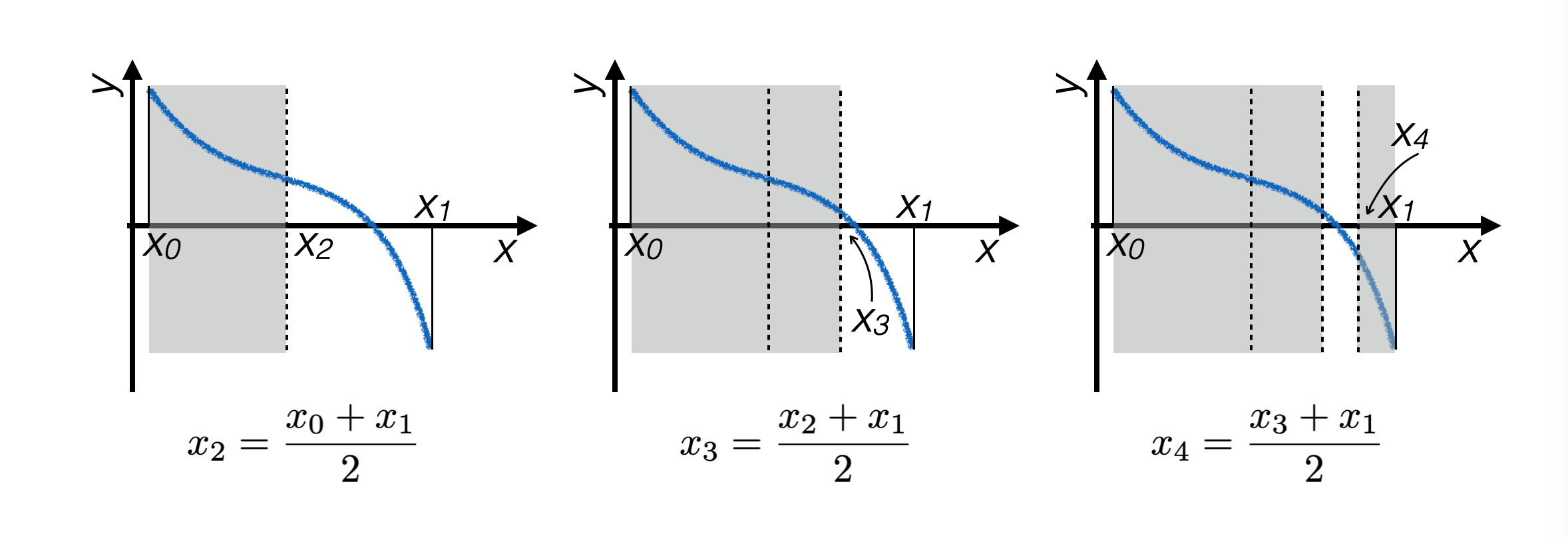

6.1.2 una implementazione dell’algoritmo di bisezione

• Ad ogni iterazione, si calcola il punto medio dell’intervallo che contiene lo zero e si decide se lo zero stia alla sua destra o alla sua sinistra

  double bisezione (
    double g (double),
    double xMin,
    double xMax,
    double precision = 0.0001
  )
  {
    double xAve = xMin ;
    while ((xMax - xMin) > precision)
      {
        xAve = 0.5 * (xMax + xMin) ;
        if (g (xAve) * g (xMin) > 0.) xMin = xAve ;
        else                          xMax = xAve ;
      }
    return xAve ;
  }  
  

  (esempio 6.0)

6.1.3 una implementazione dell’algoritmo di bisezione in modo ricorsivo

• L’algoritmo di bisezione effettua ripetutamente la stessa operazione in maniera ricorsiva

• Questo comportamento si può anche implementare in C++, scrivendo una funzione ricorsiva, cioè che invoca se stessa:

  double bisezione_ricorsiva (
    double g (double),
    double xMin,
    double xMax,
    double precision = 0.0001
  )
  {
    double xAve = 0.5 * (xMax + xMin) ;
    if ((xMax - xMin) < precision) return xAve ;
    if (g (xAve) * g (xMin) > 0.) return bisezione_ricorsiva (g, xAve, xMax, precision) ;
    else                          return bisezione_ricorsiva (g, xMin, xAve, precision) ;
  }  
  

Attenzione

In ogni funzione ricorsiva, devono essere presenti due elementi:

• L’invocazione della funzione stessa

• La condizione di uscita dalla sequenza di auto-invocazioni

(esempio 6.1)

6.2 la ricerca di estremanti: il metodo della sezione aurea

Ipotesi semplici

• Funzione g(x) continua definita su un intervallo compatto e connesso [x₀, x₁]

• la funzione ha un solo estremante nell’intervallo

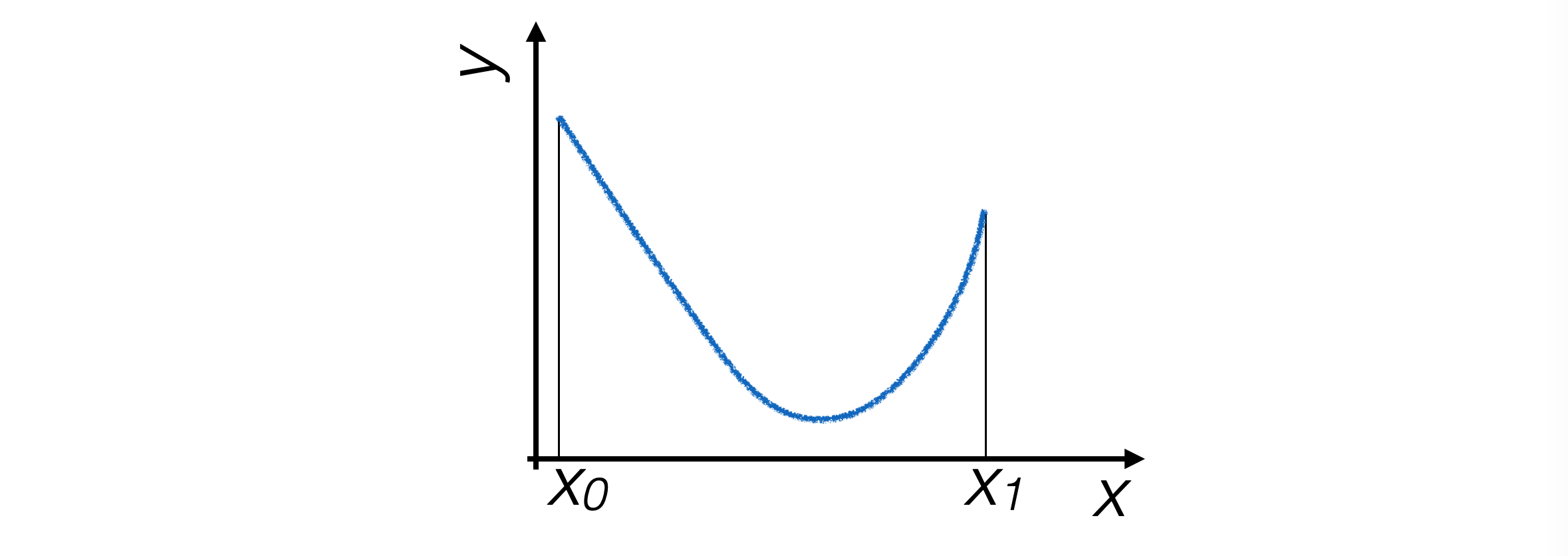
• Anche in questo caso si procede per passi, restringendo ad ogni iterazione l’intervallo che contiene l’estremante fino a che diventa più piccolo di una precisione prefissata

6.2.1 il criterio di restringimento

• Per trovare il minimo di una funzione servono abbastanza punti da capirne la pendenza in diverse regioni dell’intervallo, quindi se ne cercano quattro, che determinano tre intervalli

• L’intervallo si stringe eliminando il tratto dove il minimo di sicuro non c’è.

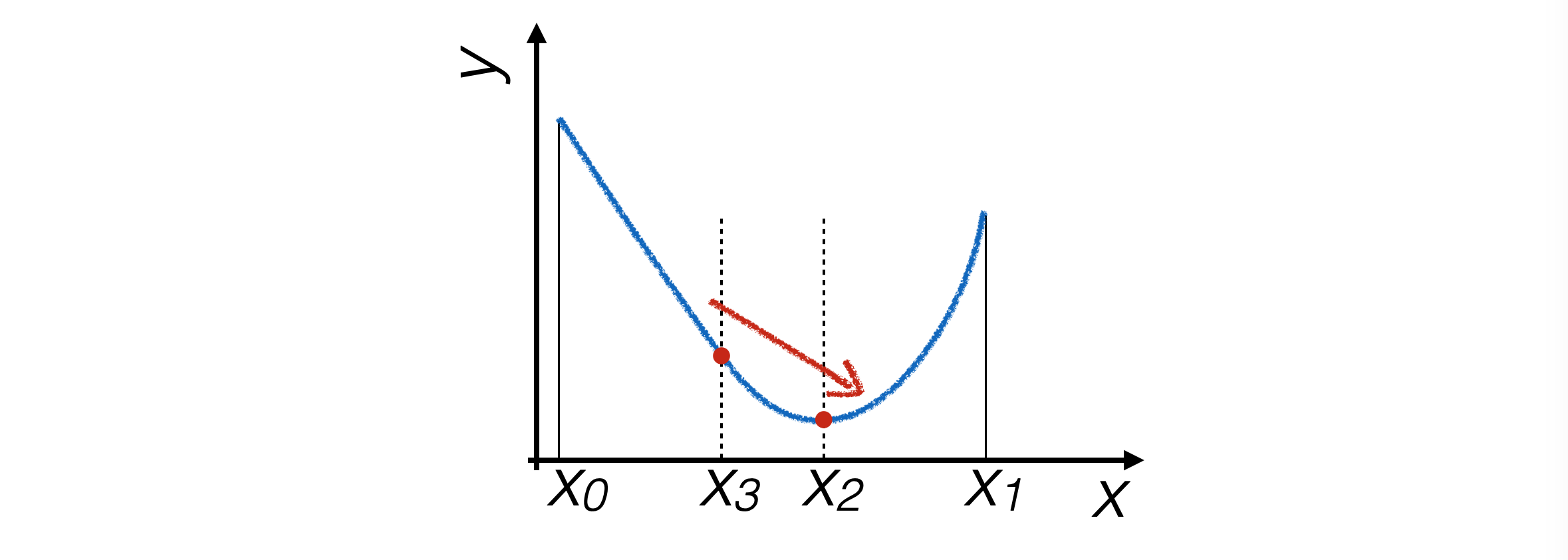
• L’iterazione successiva si restringe a \([x_3,x_1]\) se \(g(x_3) > g(x_2)\), altrimenti si restringe a \([x_0, x_2]\)

6.2.2 l’ottimizzazione della scelta dei punti

• Per ottimizzare il calcolo, i punti \(x_2, x_3\) vengono scelti in modo che uno dei due possa essere utilizzato anche nell’iterazione seguente, garantendo la stessa proporzione di suddivisione dell’intervallo

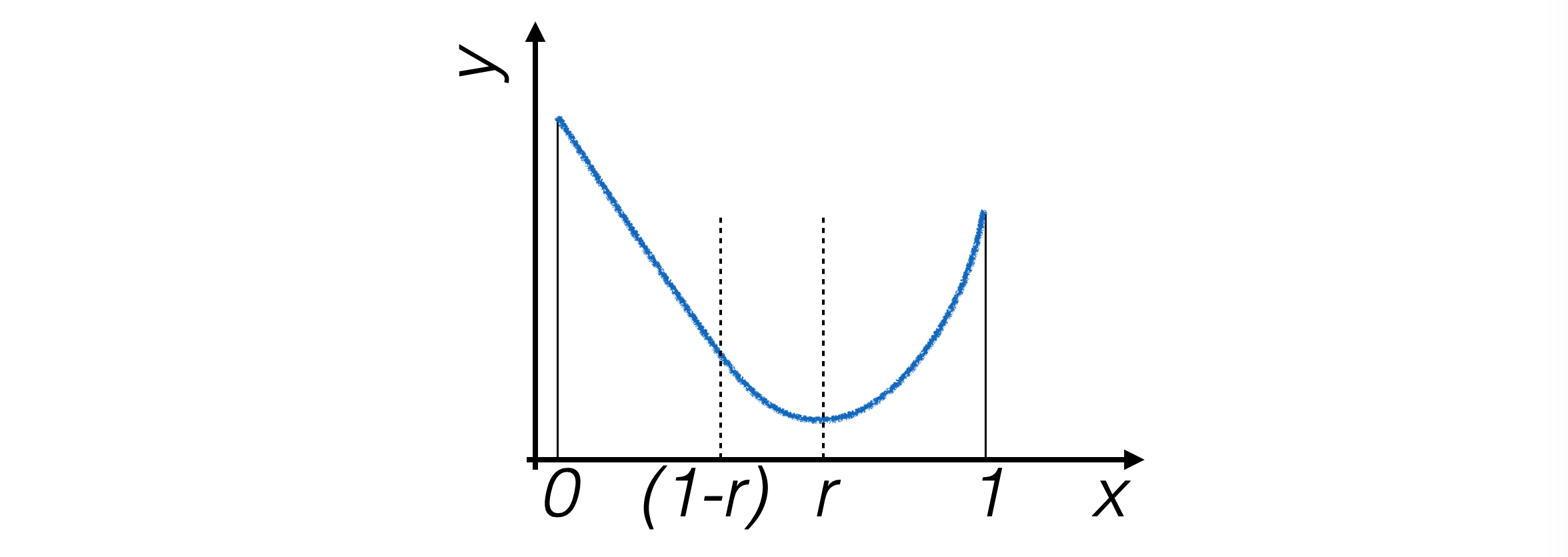
• Perché questo sia possibile deve valere:

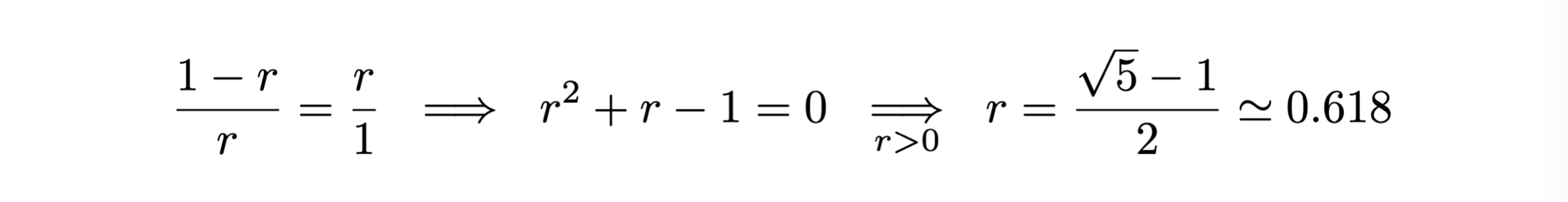
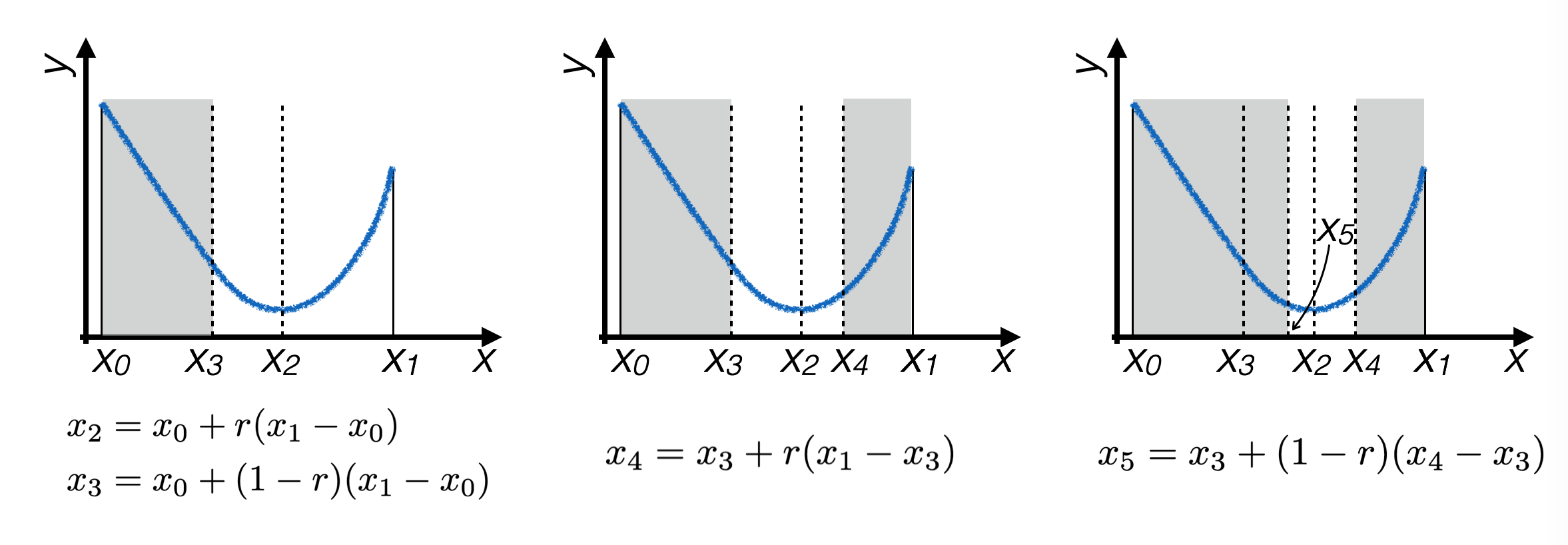
• Dunque il processo iterativo si restringe intorno all’estremante della funzione:
  

6.3 mettere tutto insieme

• Esistono molte tecniche di ricerca di zeri ed estremanti di funzioni, che sono spesso il nocciolo duro di software di analisi dati

• Una collezione di algoritmi si trova nel volume numerical recipes

• Oltre al problema locale di compiere operazioni in condizioni di buona regolarità, algoritmi generici devono anche trovare il modo di ricondurre un problema generale a casi semplici

  • Ad esempio, nel caso della ricerca di minimi bisogna evitare che gli algoritmi trovino minimi locali e non identifichino il minimo globale di una funzione

• La funzionalità di un algoritmo dipende criticamente dalla dimensione dello spazio di definizione delle funzioni

6.4 il disegno di funzioni e punti in ROOT

• una funzione matematica in ROOT si implementa con la classe TF1

  TF1 fa1 ("fa1", "sin(x)/x", 0, 10) ;
  TCanvas c1 ;
  fa1.Draw () ;
  

  • esistono molti modi di definire un oggetto di tipo TF1, sia a partire dalla forma analitica delle funzioni che da una funzione scritta in C++, descritti nelle pagine di documentazione di ROOT

• un punto si disegna con la classe TMarker:

  TMarker punto (5., 0.5, 20) ;
  

(esempio 6.2)

6.5 ESEMPI

• Gli esempi relativi alla lezione si trovano qui

6.6 ESERCIZI

• Gli esercizi relativi alla lezione si trovano qui

previous

Soluzioni: Lezione 5

next

Esempi: Lezione 6