.md .pdf

Contents

Lezione 9: la verosimiglianza

Indice

• 9.1 La verosimiglianza

  • 9.1.1 Un modello che descrive i dati

  • 9.1.2 Distribuzioni di probabilità

• 9.2 Il logaritmo della massima verosimiglianza

• 9.3 La costruzione di una likelihood

  • 9.3.1 La distribuzione di probabilità e la funzione di likelihood

• 9.4 Il disegno di una funzione di C++ con ROOT

  • 9.4.1 La creazione di un oggetto di tipo TF1

  • 9.4.2 La preparazione della funzione TF1

• 9.5 ESEMPI

• 9.6 ESERCIZI

9.1 La verosimiglianza

• Tutta l’informazione che caratterizza un esperimento, che riassume sia le assunzioni teoriche che le misure effettuate, è inscritta nella verosimiglianza o likelihood, definita come il prodotto del valore della distribuzione di densità di probabilità calcolata per ogni misura effettuata:

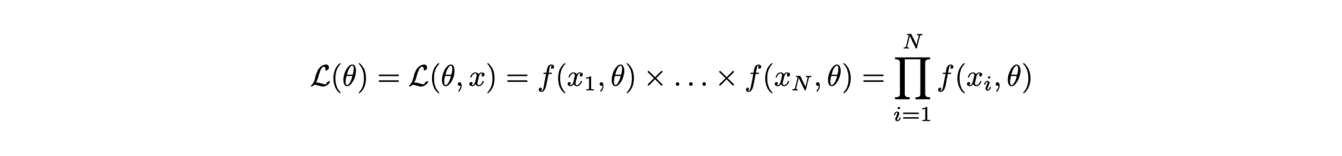
• La likelihood è funzione sia delle misure che dei parametri, tuttavia si evidenzia la dipendenza dai parametri perché a misure finite i dati sono immutabili.

9.1.1 Un modello che descrive i dati

• Un modello è una distribuzione di probabilità f o una legge g alla quale ci si aspetta che le misure obbediscano.

• I risultati delle misure sono variabili rispetto alle quali il modello dipende

• Eventuali parametri da cui dipende il modello, che non sono misurati, sono detti parametri.

9.1.2 Distribuzioni di probabilità

• Dato un insieme di misure reali x_i definite su un insieme Ω indipendenti identicamente distribuiite, sappiamo che seguono una data distribuzione di densità probabilità, indicata genericamente come f(x, θ)

• Questo significa che f(x_i, θ) è la densità di probabilità che la misura avvenga nel punto x_i dell’insieme di definizione Ω.

• Il simbolo θ indica che la funzione di densità di probabilità f dipende da altri parametri oltre che x

  • θ può anche essere un vettore di parametri

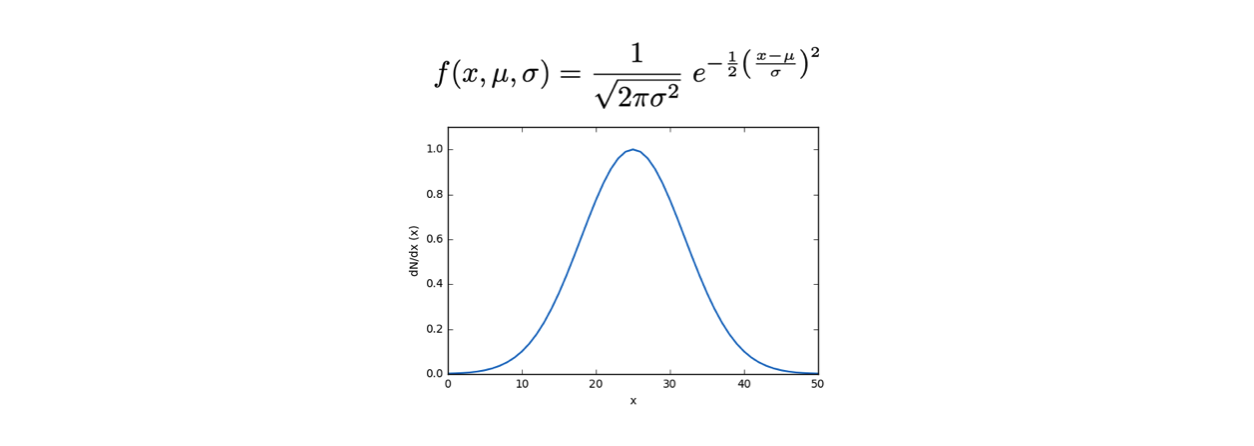
  • Ad esempio, una distribuzione Gaussiana ha due parametri aggiuntivi, μ e σ:

9.2 Il logaritmo della massima verosimiglianza

• Spesso si utilizza per fare conti e nelle rappresentazioni grafiche il logaritmo della funzione di likelihood, indicato con in lettera corsiva minuscola:.

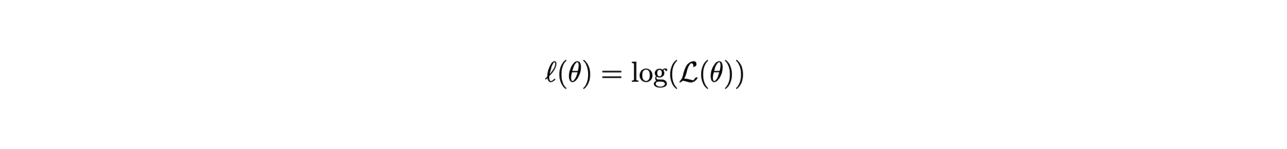
• Infatti, siccome il logaritmo è una funzione monotona crescente, il comportamento della likelihood ed il suo logaritmo sono simili

• Il logaritmo di un prodotto di termini è uguale alla somma dei logaritmi dei singoli termini

  \[\log(\mathcal{L}(\theta;\vec{x})) = \log\left(\prod_{i=1}^N f(x_i,\theta)\right) = \sum_{i=1}^N \log\left(f(x_i,\theta)\right)\]

• Il logaritmo di un numero è più piccolo del numero stesso e varia su un intervallo minore rispetto alla variabilità del numero stesso, quindi operazioni con i logaritmi possono essere stabili numericamente

9.3 La costruzione di una likelihood

• Si utilizzerà l’esempio della distribuzione esponenziale, con l’unico parametro τ come argomento aggiuntivo della verosimiglianza:

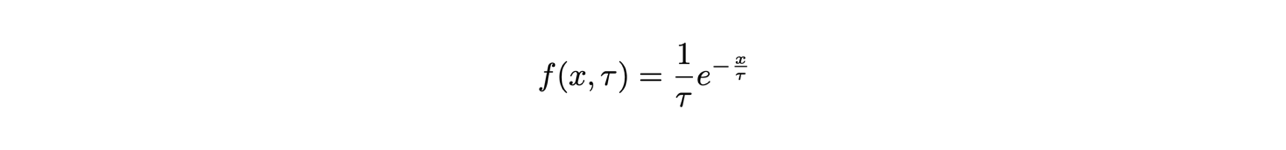
9.3.1 La distribuzione di probabilità e la funzione di likelihood

• Sia la distribuzione di densità di probabilità che il calcolo della likelihood vanno scritte in codice sorgente:

  double esponenziale (double x, double tau)
    {
       if (tau == 0.) return 1. ;
       return exp (-1. * x / tau) / tau ;
    }
  

  • il primo if serve a proteggere il programma da risultati infiniti

• il calcolo della likelihood avrà in ingresso sia i dati, che il parametro di interesse:

  double loglikelihood (
    const vector<double> & data,
    double param
  )
  {
    double result = 0. ;
    for (int i = 0 ; i < data.size () ; ++i) result += log (esponenziale (data.at (i), param)) ;
    return result ;   
  }
  

  • in questo caso, si calcola il logaritmo del valore della densità di probabilità in ogni punto

    (esempio 9.0)

9.4 Il disegno di una funzione di C++ con ROOT

• Le funzioni di C++ si disegnano in ROOT con la classe TF1

• Perché un oggetto di tipo TF1 possa essere costruito con una qualunque implementazione in formato di codice sorgente, tutte le funzioni utilizzate devono avere lo stesso prototipo, in modo che la classe TF1 sappia riconoscerne il comportamento:

  Double_t exp_R (Double_t * x, Double_t * par) ;
  

  • il primo argomento è un vettore che rappresenta il dominio della funzione: per una funzione mono-dimensionale la x quindi è x[0]

  • il secondo argomento è l’insieme dei parametri della funzione

9.4.1 La creazione di un oggetto di tipo TF1

• Per la creazione di un oggetto di tipo TF1 che disegni una funzione di C++ esiste un costruttore dedicato della classe:

  TF1::TF1 (const char * name,
            Double_t(*)(Double_t *, Double_t *) fcn,
            Double_t xmin = 0,
            Double_t xmax = 1,
            Int_t npar = 0,
            Int_t ndim = 1,
            EAddToList addToGlobList = EAddToList::kDefault
           )
  

• I parametri di interesse per noi sono i primi 5:

  • const char * name è l’identificativo interno a ROOT dell’oggetto

  • Double_t(*)(Double_t *, Double_t *) fcn è la funzione scritta in codice sorgente

  • xmin è il minimo del dominio dove viene disegnata la funzione

  • xmax è il massimo del dominio dove viene disegnata la funzione

  • npar è il numero di parametri della funzione

9.4.2 La preparazione della funzione TF1

• la chiamata al costruttore, nel caso di una funzione esponenziale, ha quindi il seguente formato:

  TF1 f_exp ("f_exp", exp_R, 0, 5 * t_zero, 1) ;
  

• il numero di parametri è 1, perché corrisponde a t₀

• per attribuire un determinato valore al parametro si usa il metodo TF1::SetParameter

  f_exp.SetParameter (0, t_zero) ;
  

  • il primo argomento è l’indice del parametro

  • il secondo argomento è il valore da impostare

• nel caso la funzione abbia più di un parametro, si può utilizzare il metodo TF1::SetParameters, che prende in ingresso un array di valori lungo quanto il numero di parametri della funzione

9.5 ESEMPI

• Gli esempi relativi alla lezione si trovano qui

9.6 ESERCIZI

• Gli esercizi relativi alla lezione si trovano qui

previous

Soluzioni: Lezione 8

next

Esempi: Lezione 9