.md .pdf

Contents

Lezione 3: visualizzazione di dati con ROOT

Indice

• 3.1 Introduzione

  • 3.1.1 l’organizzazione delle librerie di ROOT

  • 3.1.2 prerequisiti per utilizzare ROOT

  • 3.1.3 come compilare un programma che include classi di ROOT

• 3.2 TH1F: istogrammi monodimensionali

  • 3.2.1 i bin di un istogramma

  • 3.2.2 istogrammi monodimensionali e distribuzioni di densità di probabilità

  • 3.2.3 istogrammi monodimensionali in ROOT

  • 3.2.4 riempimento di un TH1F

  • 3.2.5 visualizzazione di un TH1F

  • 3.2.6 opzioni grafiche

  • 3.2.7 scale logaritmiche

  • 3.2.8 le statistiche di un istogramma

• 3.3 Un utile intermezzo: la lettura di un file di testo

  • 3.3.1 L’implementazione della lettura

• 3.4 una piccola digressione: la varianza di una distribuzione

  • 3.4.1 la varianza e la dimensione del campione

  • 3.4.2 varianza e misure (o numeri pseudo-casuali)

  • 3.4.3 incertezza sulla media

• 3.5 TH2F: istogrammi bidimnesionali

• 3.6 L’interfaccia interattiva di ROOT: la classe TApplication

• 3.7 Una gestione furba del testo: TString

• 3.8 ESEMPI

• 3.9 ESERCIZI

3.1 Introduzione

• ROOT offre un insieme di strumenti di visualizzazione, analisi e salvataggio dati sviluppati nell’ambito della fisica delle particelle elementari

• gli strumenti sono scritti in C++ ed esiste l’interfaccia Python per utilizzarli, con adattamenti al formato dei dati alla sintassi tipica di quell’ambiente

• ROOT offre anche un ambiente interattivo che si presenta nella forma di una linea di comando, dove istruzioni scritte in C++ vengono interpretate da un parser dedicato

• In questo corso vi mostriamo alcune funzionalità di ROOT, la descrizione completa di quello che può fare si trova nella documentazione on-line

3.1.1 l’organizzazione delle librerie di ROOT

• in un programma scritto in C++, ogni oggetto di ROOT viene reso disponibile nel codice sorgente con il corrispondente comando #include

• la maggior parte degli strumenti disponibili sono implementati sotto forma di classi

  #include "TH1F.h"
  
  int main (int argc, char ** argv)
    {
      TH1F istogramma ("istogramma", "istogramma", 10, -3., 3.) ;
      return 0 ;
    }
  

• la visualizzazione degli strumenti statistici è un aspetto fondamentale del programma, quindi molte opzioni grafiche sono integrate negli oggetti statistici

• Il software e la documentazione di ROOT si trovano a questo indirizzo web.

3.1.2 prerequisiti per utilizzare ROOT

• dopo l’installazione, le librerie di ROOT sono salvate nel disco fisso solitamente in una cartella dedicata

• per avviare l’interfaccia interattiva e per conoscere dove stiano le librerie, è necessario che:

  • la cartella che contiene l’eseguibile root faccia parte della lista di indirizzi salvati nella variabile d’ambiente della SHELL $PATH

  • la cartella che contiene le librerie precompilate faccia parte della lista di indirizzi salvati nella variabile d’ambiente della SHELL $LD_LIBRARY_PATH

• esiste lo script thisroot.sh nelle cartelle di installazione che va richiamato per effettuare tali impostazioni:

  > source thisroot.sh
  

3.1.3 come compilare un programma che include classi di ROOT

• è necessario fornire al compilatore opzioni aggiuntive perché sia in grado di trovare tutti i file da includere e tutte le librerie da compilare

• la lista di opzioni aggiuntive si visualizza con il seguente comando di SHELL:

  > root-config --cflags --glibs  
  

• per evitare di copiare ed incollare il suo output nel comando di compilazione, si può includere la sua chiamata direttamente nel programma di compilazione, utilizzando gli apici inversi:

  > c++ -o main_00 `root-config --glibs --cflags` main_00.cpp
  

  (esempio 3.0)

3.2 TH1F: istogrammi monodimensionali

• gli istogrammi sono una rappresentazione di distribuzioni differenziali, costruita a partire da un campione di numeri, che chiamiamo eventi

• si parte quindi da un campione di eventi {x_i}_i=1,..,N

  • un esempio di un campione di eventi è l’insieme delle misure raccolte durante un esperimento, oppure una sequenza di numeri pseudo-casuali

3.2.1 i bin di un istogramma

• per una variabile casuale di interesse x, si suddivide il suo intervallo di definizione in sotto-intervalli adiacenti e disgiunti delimitati da {x_k}

  • l’intervallo k-esimo è limitato fra x_k ed x_k+1

  • solitamente gli intervalli sono chiamati bin

• un istogramma è l’insieme dei conteggi degli eventi che cascano in ogni intervallo

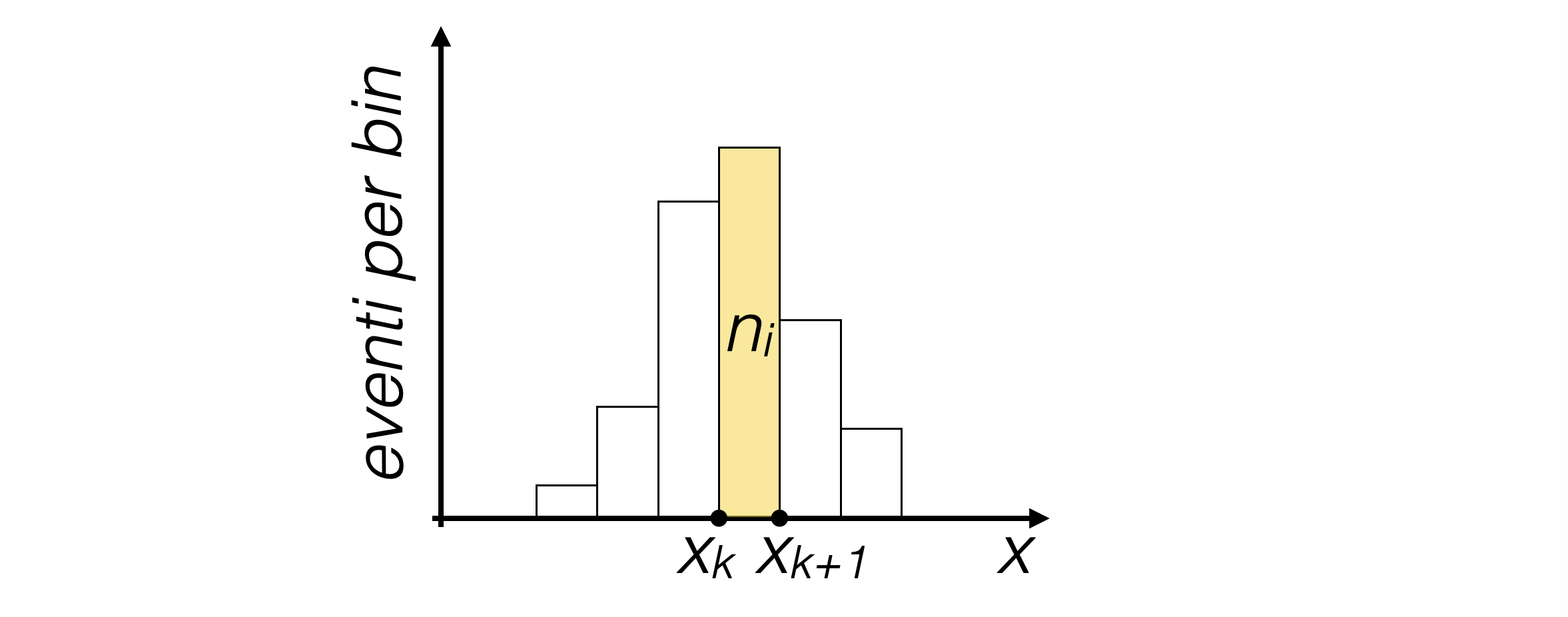
• la visualizzazione di un istogramma mono-dimensionale mostra tipicamente:

  • sull’asse orizzontale l’intervallo di definizione della variabile x

  • sull’asse verticale i conteggi corrispondenti a ciascun bin

  • sopra ad ogni bin, una barra verticale alta quanto i conteggi

3.2.2 istogrammi monodimensionali e distribuzioni di densità di probabilità

• al limite per la dimensione dei bin che diventa infinitesima, un istogramma diventa una funzione continua

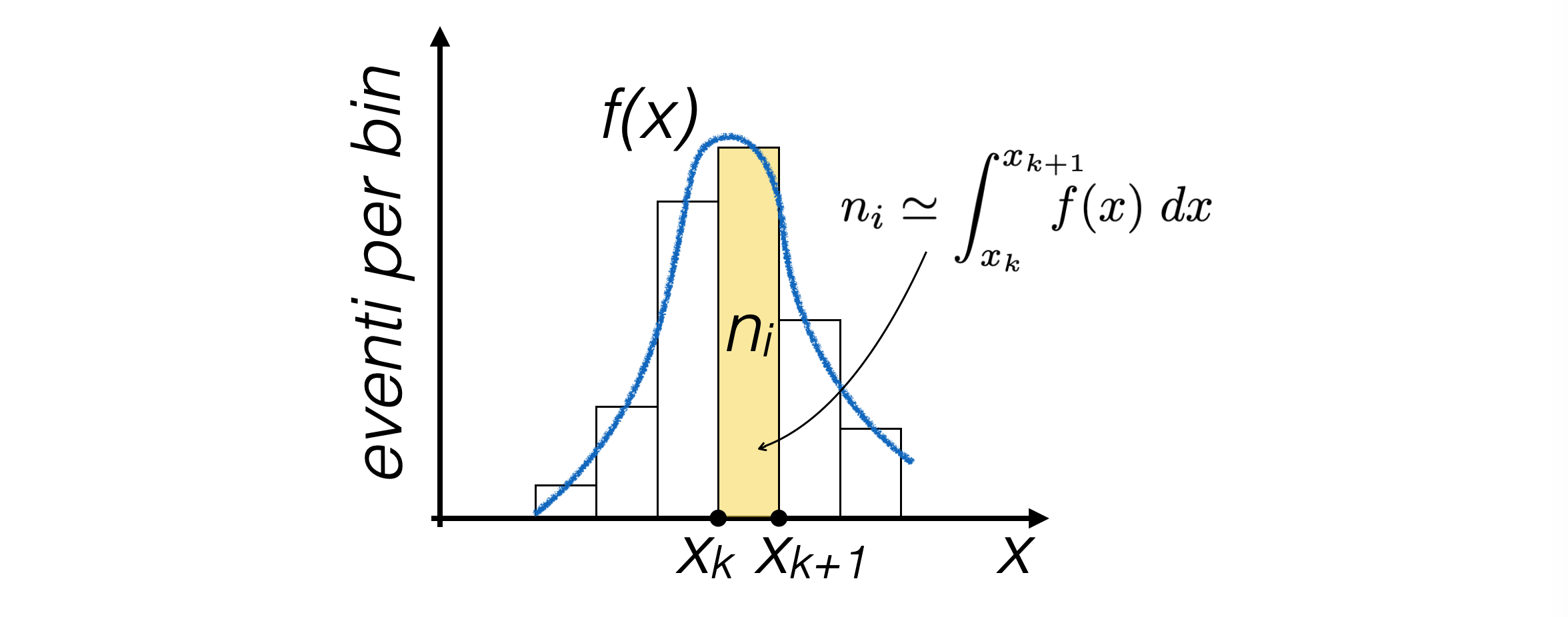
• se si dividesse il contenuto di ogni bin per il numero totale di eventi N, questa funzione è normalizzata, quindi un istogramma diventa l’approssimazione di una distribuzione di densità di probabilità

3.2.3 istogrammi monodimensionali in ROOT

• istogrammi mono-dimensionali in ROOT sono realizzati con la classe TH1F

  TH1F istogramma ("istogramma", "titolo", 10, -3., 3.) ;
  

• il costruttore di TH1F prende come input:

  • un nome: è saggio usare il medesimo della variabile (ogni oggetto deve avere un nome unico!)

  • un titolo, che viene scritto sopra l’istogramma

  • il numero di bin (10 in questo caso) in cui dividere l’intervallo di definizione della variabile

  • l’intervallo di definizione della variabile (-3., 3. in questo caso)

3.2.4 riempimento di un TH1F

• un oggetto della classe TH1F quando viene creato è vuoto, cioè i conteggi di ogni singolo bin sono nulli

• per riempire l’istogramma si utilizza il suo metodo Fill, che viene chiamato per ogni evento (esempio 3.1):

  istogramma.Fill (2.2) ;
  istogramma.Fill (2.1) ;
  istogramma.Fill (-1.4) ;
  

  • aggiorna i conteggi del bin in cui casca il valore passato (in questo caso 2.2, 2.1, -1.4)

  • aggiorna i contatori per il calcolo delle statistiche (numero di eventi, somma degli eventi, somma del quadrato degli eventi)

3.2.5 visualizzazione di un TH1F

• per visualizzare un istogramma, serve istanziare un oggetto grafico della classe TCanvas, che è la tela dove l’istogramma viene disegnato

  • è necessario includere TCanvas.h perché il programma compili

  TCanvas c1 ;
  istogramma.Draw () ;
  c1.Print ("esempio.png", "png") ;
  

  • l’oggetto c1 si occupa di produrre l’immagine che contiene l’istogramma

• il box in alto a sinistra nell’immagine dell’istogramma riporta statistiche associate alla collezione di eventi

(esempio 3.2)

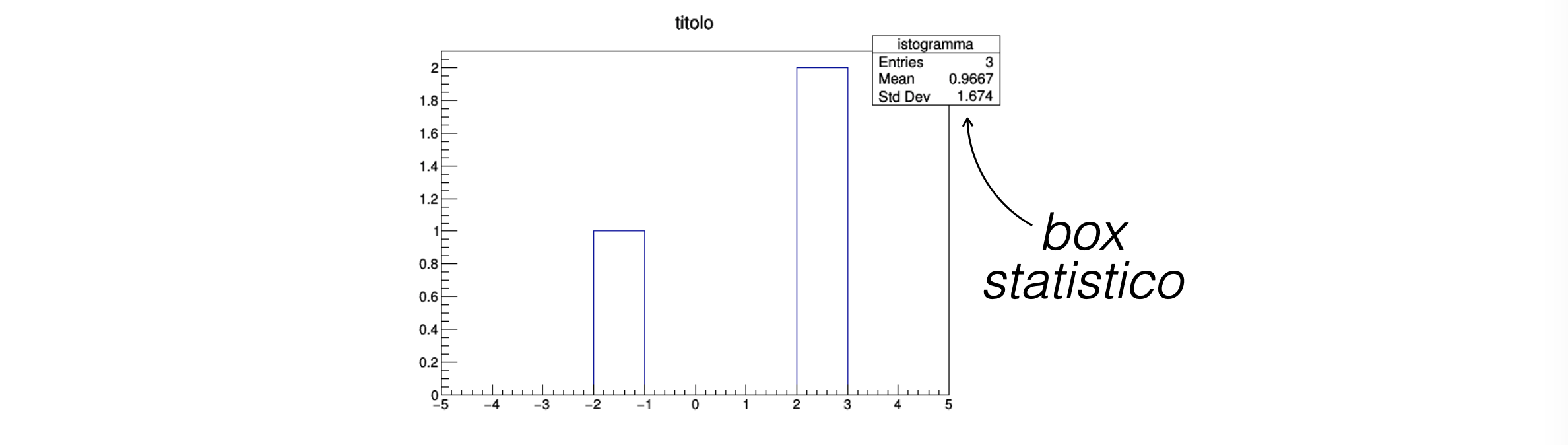
3.2.6 opzioni grafiche

• perché l’informazione sull’istogramma sia completa, è necessario aggiungere informazioni riguardo il significato degli assi, prima di invocare il metodo Draw:

  istogramma.GetXaxis ()->SetTitle ("asse x") ;
  istogramma.GetYaxis ()->SetTitle ("conteggi per bin") ;
  

• inoltre, è possibile cambiare il colore di riempimento di un istogramma:

  istogramma.SetFillColor (kOrange + 1) ;
  

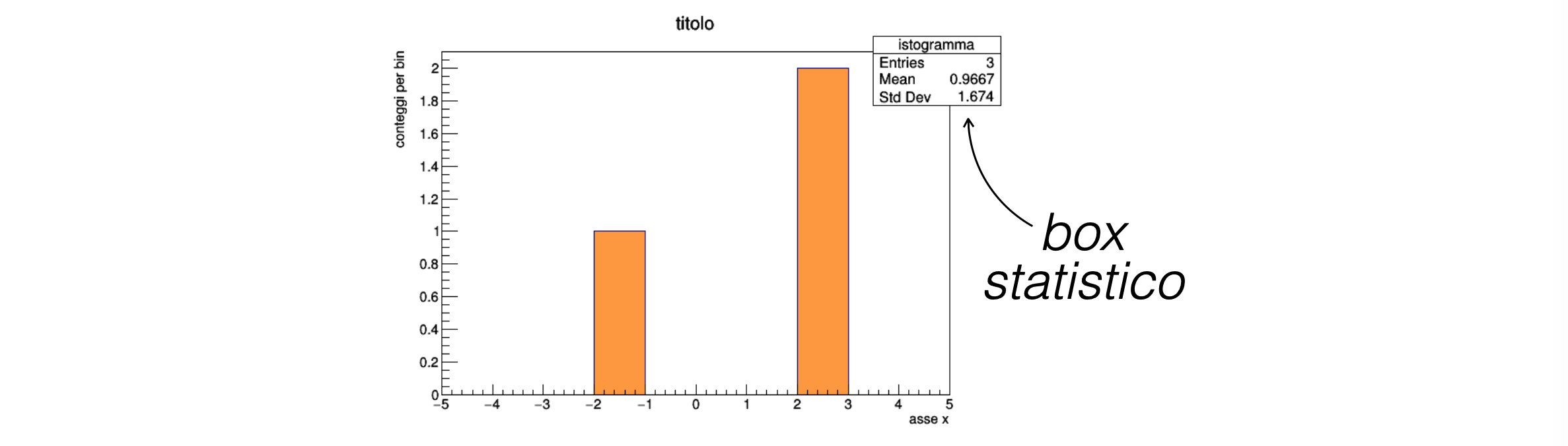
• la descrizione dettagliata di tutte le funzionalità ed opzioni di disegno degli istogrammi è documentata nella relativa guida per l’utente

(esempio 3.3)

3.2.7 scale logaritmiche

• quando i valori in diversi bin cambiano considerevolmente, può essere comodo visualizzare gli istogrammi in scala logaritmica (lungo l’asse orizzontale o verticale), per migliorare la leggibilità del risultato

• essendo una diversa visualizzazione dello stesso contenuto, è un’operazione che si fa con un metodo della classe TCanvas

  c1.SetLogy () ;
  c1.Print ("Gaussian.png", "png") ;
  

  • chiaramente, lo zero dell’asse in scala logaritmica non può comparire nelle immagini

(esempi 3.4 e 3.5)

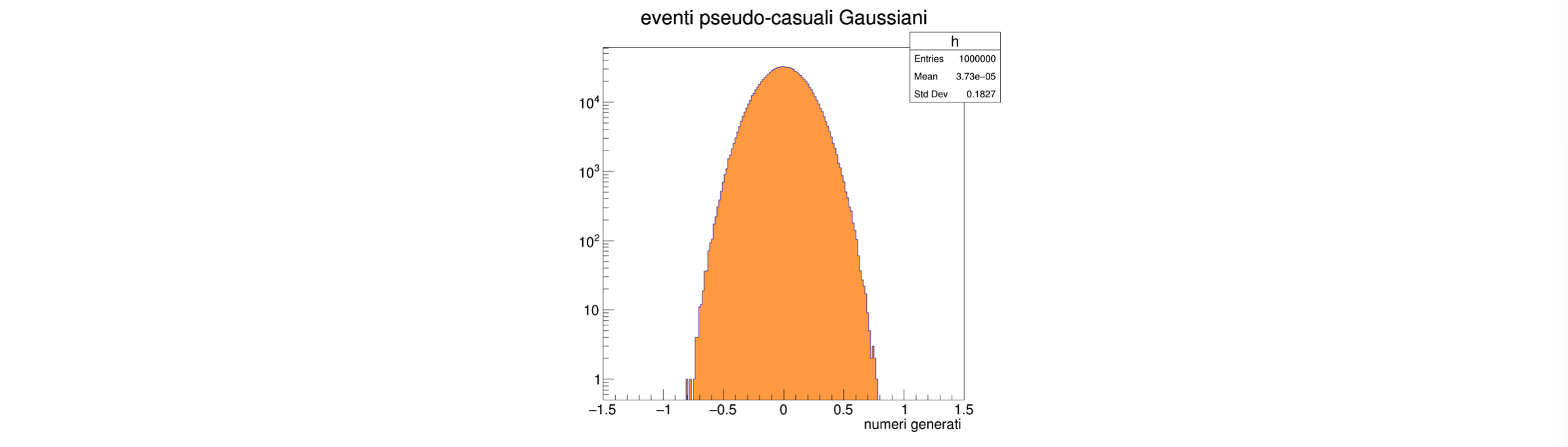
3.2.8 le statistiche di un istogramma

• è possibile estrarre i valori della media e della deviazione standard degli eventi salvati in un istogramma:

  std::cout << "numero di eventi:    " << h.GetEntries () << std::endl ;
  std::cout << "media:               " << h.GetMean ()    << std::endl ;
  std::cout << "deviazione standard: " << h.GetRMS ()     << std::endl ;
  

(esempio 3.6)

3.3 Un utile intermezzo: la lettura di un file di testo

• Può essere comodo salvare informazioni semplici su file di testo, per poterle rileggere dai programmi di analisi dati

• La gestione dell’accesso a file di testo in C++ è analoga alla scrittura a schermo e lettura da tastiera: si utilizzano gli operatori di redirezione operator>> (per leggere) ed operator<< (per scrivere) fra un oggetto che rappresenta il file e le variabili

3.3.1 L’implementazione della lettura

• L’oggetto che rappresenta un file è di tipo fstream: ifstream per lettura (input file stream) ed ofstream per scrittura (output file stream):

  #include <fstream>
  // ...
  ifstream input_file ;
  input_file.open ("file.txt", ios::in) ;
  // ...
  double input_val ;
  while (true)
    {
      input_file >> input_val ;
      if (input_file.eof () == true) break ;
    }
  input_file.close () ;
  

  • In questo modo, una sequenza di numeri scritti nel file file.txt vengono letti uno ad uno, trasferendone il valore nella variabile input_val

  • All’interno del file di testo, i valori sono seperati da spazi, tab o accapo.

  • Al termine della lettura, il file viene chiuso.

3.4 una piccola digressione: la varianza di una distribuzione

• dato un campione di variabili casuali {x_i}_i=1,..,N indipendenti identicamente distribuite, la varianza della distribuzione è la media degli scarti quadratici dalla media

• si dimostra che la varianza di un campione è uguale alla media dei quadrati meno il quadrato della media: V = E[x²]-E[x]² (E[f] è il valore di aspettazione di f sul campione in esame)

• la radice della varianza è detta sigma, o deviazione standard ed è una stima della dispersione del campione attorno alla sua media

(esempio 3.7)

3.4.1 la varianza e la dimensione del campione

• all’aumentare del numero di eventi nel campione, la dispersone degli eventi non cambia, quindi la varianza rimane costante per variabili identicamente distribuite

• chiaramente, siccome ogni campione è finito, i valori della varianza ottenuti con campioni diversi non sono identici, ma ci si aspetta che siano compatibili fra loro

• di conseguenza, anche la deviazione standard non dipende dal numero di eventi nel campione

(esempi 3.8 e 3.9)

3.4.2 varianza e misure (o numeri pseudo-casuali)

• se si conosce media e varianza di un campione, si ha un’idea di dove ci si aspetta di trovare l’evento successivo di quel campione

• se il campione è un insieme di misure, la deviazione standard dice quanto distante ci si aspetta di trovare la prossima misura dalla media delle misure raccolte

• dunque, la deviazione standard è associata all’incertezza sulla singola misura

3.4.3 incertezza sulla media

• all’aumentare del numero di misure, invece, aumenta la precisione con la quale si conosce la media del campione

• la deviazione standard della media, definita come la deviazione standard divisa per la radice del numero di eventi nel campione, è una stima dell’incertezza sulla media

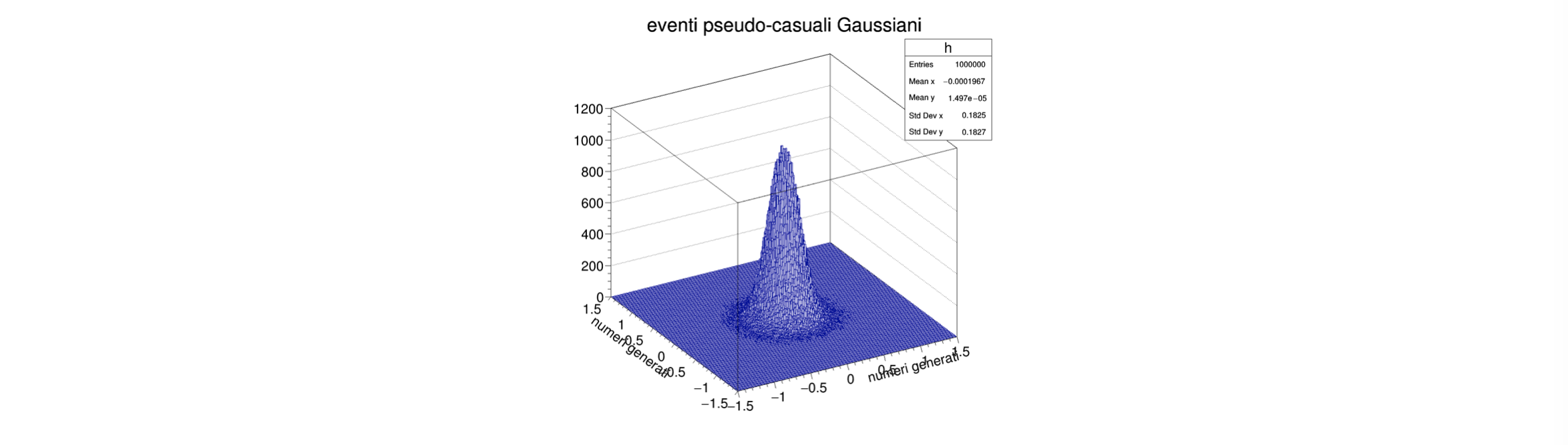
3.5 TH2F: istogrammi bidimensionali

• il concetto di istogramma monodimensionale si applica facilmente anche al caso bidimensionale

• l’oggetto di ROOT associato a questo concetto si chiama TH2F

• nel costruttore, è necessario inserire numero di bin ed estremi per due direzioni

  TH2F h2 ("h2", "eventi pseudo-casuali Gaussiani", 200, -1.5, 1.5, 200, -1.5, 1.5) ;
  

• nel riempimento, il metodo TH2F::Fill (Double_t x, Double_t y) prende in ingresso due valori

  h2.Fill (rand_TCL (-1., 1., 10), rand_TCL (-1., 1., 10)) ;
  

(esempio 3.10)

3.6 L’interfaccia interattiva di ROOT: la classe TApplication

• i TCanvas di ROOT sono dotati di diverse funzionalità interattive alle quali si accede con menu a tendina o contestuali (accessibili con il pulsante destro del mouse)

• per abilitare queste funzionalità in un programma compilato, è necessario utilizzare un oggetto della classe TApplication

  TApplication theApp ("theApp", &argc, argv) ;
  TCanvas c1 ;
  istogramma.Draw ("hist") ;
  theApp.Run () ;
  

  • fra la linea

    TApplication theApp ("theApp", &argc, argv) ;
    

    e la linea

    theApp.Run () ;
    

    va incluso tutto il codice che si vuole interattivo

  • può esistere un solo oggetto di tipo TApplication in ogni programma

  • per terminare l’esecuzione del programma, da un qualunque TCanvas bisogna utilizzare il menu File->Quit ROOT

(esempio 3.11)

3.7 Una gestione furba del testo: TString

• ROOT fornisce un oggetto che serve per maneggiare stringhe che può essere utilizzato come argomento nei metodi delle sue classi

• le TString hanno definite una serie di operazioni che permettono di combinare velocemente testo con altre variabili

  int num = atoi (argv[1]) ;
  TString titolo = "ci sono " ;
  titolo += num ;
  titolo += " eventi" ;
  TH1F istogramma ("istogramma", titolo, 10, -3., 3.) ;
  

(esempio 3.12)

3.8 ESEMPI

• Gli esempi relativi alla lezione si trovano qui

3.9 ESERCIZI

• Gli esercizi relativi alla lezione si trovano qui

previous

Soluzioni: Lezione 2

next

Esempi: Lezione 3