Contents

Lezione 4: la generazione di numeri pseudo-casuali

Lezione 4: la generazione di numeri pseudo-casuali

4.1 I numeri pseudo-casuali

  • quando si effettua una qualunque misura, si porta a termine il confronto fra i dati raccolti e un modello della natura

    • per falsificare il modello, oppure

    • per determinare il valore (e l’incertezza associata) di uno dei suoi parametri

  • è cruciale saper calcolare le previsioni di un modello

    • spesso non si conosce il modello in forma analitica e si ricorre a metodi computazionali alternativi per ottenere le previsioni da confrontare con le misure

  • molte tecniche di calcolo si basano sulla generazione di numeri casuali

    • per riprodurre la natura aleatoria delle misure

    • o per popolare uniformemente spazi fasi definiti entro confini sofisticati

linea

4.1.1 sequenze casuali

  • un processo casuale, o stocastico, produce una successione di numeri distribuiti casualmente secondo una distribuzione di probabilità fissata

  • la probabilità che un determinato numero compaia in qualunque punto della successione non dipende dai numeri che lo precedono o che lo seguono

  • ad esempio:

    • il tempo di arrivo di raggi cosmici su un rivelatore di muoni

    • il risultato del lancio di una moneta o di un dado

  • siccome dipendono dalle tempistiche di processi naturali, si tratta tipicamente di sequenze che richiedono molto tempo per essere costruite, che diventa un fattore limitante nei calcoli

linea

4.1.2 sequenze pseudo-casuali

  • esistono programmi e librerie, detti in generale generatori di numeri pseudo-casuali, che producono successioni di numeri tali da sembrare numeri casuali

  • la sequenza dei numeri nelle successioni è deterministica, e le funzioni utilizzate per la generazione sono costruite per mimare il comportamento di successioni casuali

  • il primo numero di una successione (o sequenza) di numeri pseudo-casuali si chiama seed, perché noto quel numero e l’algoritmo di generazione si può riprodurre l’intera sequenza

    • chiaramente, da diversi seed iniziano sequenze di numeri pseudo-casuali diverse

linea

4.1.3 il generatore lineare congruenziale

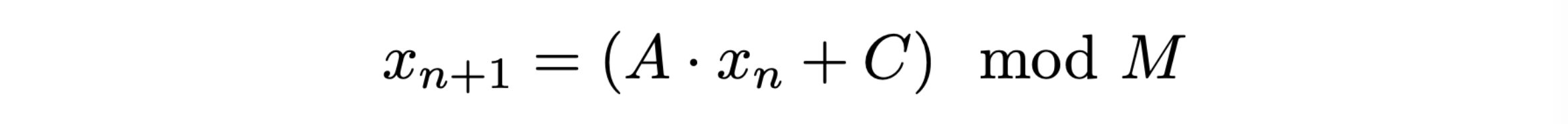
  • un esempio di formula per calcolare l’elemento successivo di una sequenza pseudo-casuale dato un qualunque numero è il seguente: lineare-congruenziale

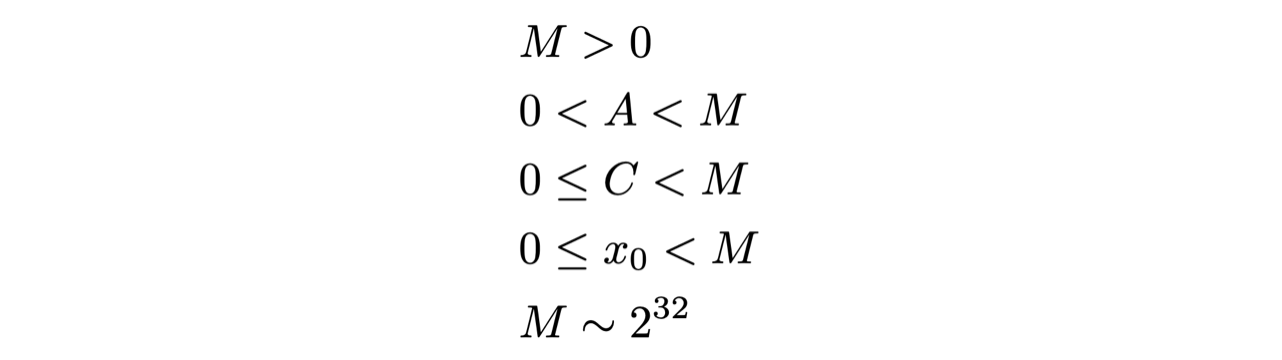
  • con: lineare-congruenziale_condizioni

  • il primo elemento della sequenza, con indice zero, è il seed

  • questo algoritmo genera per costruzione numeri compresi fra 0 ed M

linea

4.1.4 le problematiche dei generatori di numeri pseudo-casuali

  • la dipendenza funzionale fra due numeri pseudo-casuali consecutivi non deve essere visibile

  • se in una sequenza di numeri pseudo-casuali ricompare un numero già visto, la sequenza inizia a ripetersi da quel punto: si tratta della periodicità del generatore.

  • il periodo deve essere molto maggiore della quantità di numeri pseudo-casuali generati e non dipendere dalla scelta del seed

  • tipicamente i generatori di numeri casuali seguono una distribuzione uniforme: la non-uniformità della distribuzione è un altro difetto tipico che si vuole evitare

  • un esempio del risultato di un generatore di numeri pseudo-casuali poco performante si trova qui pseudo_fail

linea

4.1.5 un generatore di numeri casuali in C++

  • nella libreria cstdlib è presente un generatore di numeri pseudo-casuali rand():

    #include <cstdlib>
#include <iostream>

int main (int argc, char ** argv)
  {
    for (int i = 0 ; i < 5 ; ++i)
      std::cout << "indice " << i << " --> " << rand () << "\n" ;
    std::cout << "\nRAND_MAX: " << RAND_MAX << std::endl ;
    return 0 ;
  }

    il codice precedente produce come output:

    indice 0 --> 16807
indice 1 --> 282475249
indice 2 --> 1622650073
indice 3 --> 984943658
indice 4 --> 1144108930

RAND_MAX: 2147483647
    (esempio 4.0)

linea

4.1.6 le caratteristiche di rand ()

  • è un generatore di numeri interi pseudo-casuali distribuiti uniformemente fra 0 e RAND_MAX, che è una variabile definita all’interno della libreria cstdlib

  • il generatore inizia sempre dallo stesso seed per generare gli eventi, quindi se si rigira il programma si ottiene sempre la medesima sequenza numerica

linea

4.1.7 come cambiare il seed di generazione

  • esiste la funzione srand (int seed) che imposta il seed di generazione dei numeri casuali:

    srand (3) ;
for (int i = 0 ; i < 5 ; ++i)
  std::cout << "indice " << i << " --> " << rand () << "\n" ;

  • è importante poter riprodurre la stessa sequenza di numeri pseudo-casuali a scopo di test

  • se invece si vuole produrre ad ogni esecuzione una sequenza differente, si può utilizzare il tempo di esecuzione come seed di generazione, utilizzando la funzione time () della libreria ctime:

    #include <ctime>
// resto del codice
srand (time (NULL)) ;
for (int i = 0 ; i < 5 ; ++i)
  std::cout << "indice " << i << " --> " << rand () << "\n" ;

  • a meno di avere importanti ragioni per fare diversamente, il seed si inizializza una volta sola durante l’esecuzione di un programma

    (esempio 4.1)

linea

4.2 generare numeri pseudo-casuali con distribuzione uniforme

  • rand() genera numeri interi compresi fra 0 e RAND_MAX

  • può però essere usata per produrre sequenze di numeri pseudo-casuali che seguano distribuzioni differenti, mediante opportuni algoritmi

  • in generale le densità di probabilità dei numeri pseudo-casuali prodotti con un calcolatore avranno sempre dominio limitato, per via delle limitazioni intrinseche dei calcolatori

  • la distribuzione uniforme di numeri casuali è un caso particolare infatti è definita su un insieme limitato per costruzione (altrimenti il suo integrale sarebbe divergente)

linea

4.2.1 una distribuzione uniforme di numeri razionali pseudo-casuali

  • l’obiettivo è produrre numeri casuali compresi nell’intervallo min, max, partendo dalle risorse che abbiamo, cioè rand ()

    1. distribuzione uniforme fra 0 ed 1 :

      rand () / static_cast<float> (RAND_MAX) ;

    2. dilatazione fra 0 e max-min:

      (max - min) * rand () / static_cast<float> (RAND_MAX) ;

    3. traslazione di min:

      float rand_range (float min, float max)
  {
    min + (max - min) * rand () / static_cast<float> (RAND_MAX) ;
  }
    (esempio 4.2)

linea

4.3 altre distribuzioni di probabilità: try-and-catch

  • nel caso della distribuzione di densità di probabilità (pdf) uniforme, la probabilità che eventi pseudo-casuali vengano generati in un dato intervallo non dipende dalla posizione dell’intervallo

  • per pdf non uniformi questo non è vero

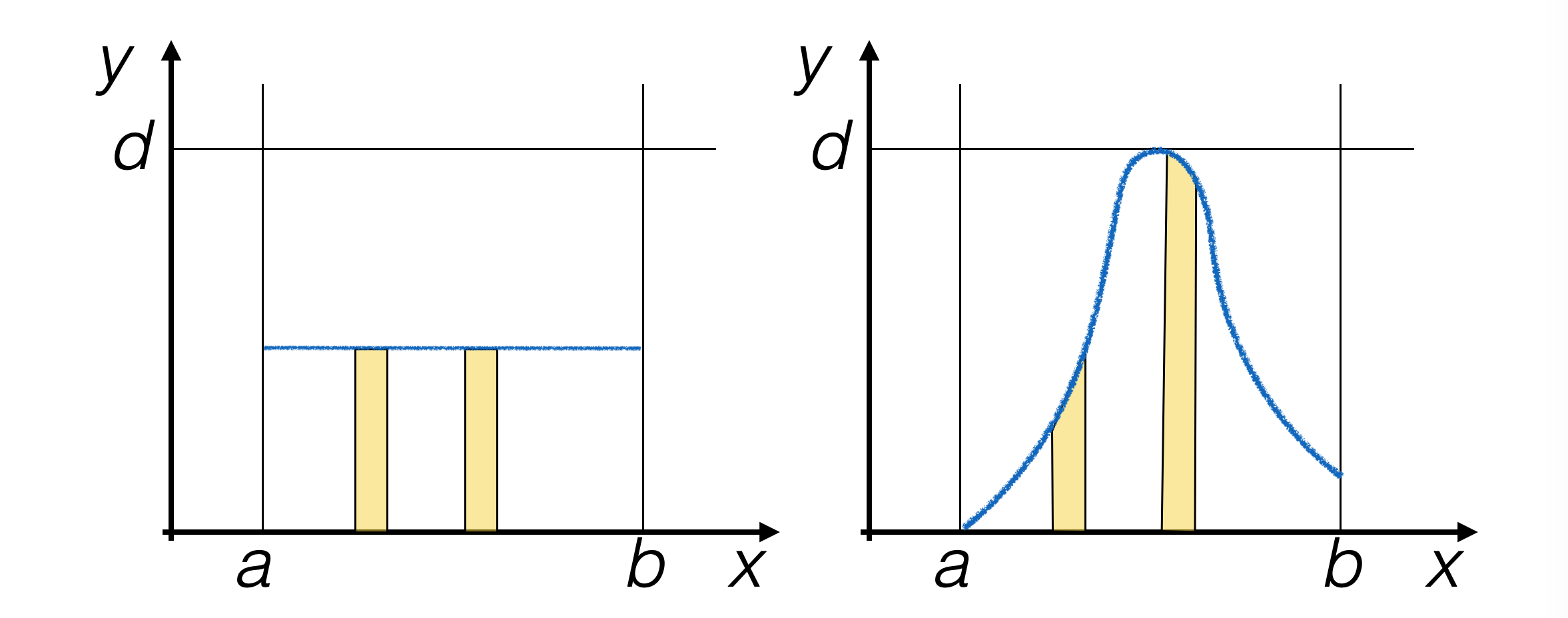
distribuzione_non_uniforme

linea

4.3.1 l’algoritmo try-and-catch (TAC)

  • generare eventi pseudo-casuali in modo proporzionale all’area sottesa dalla pdf

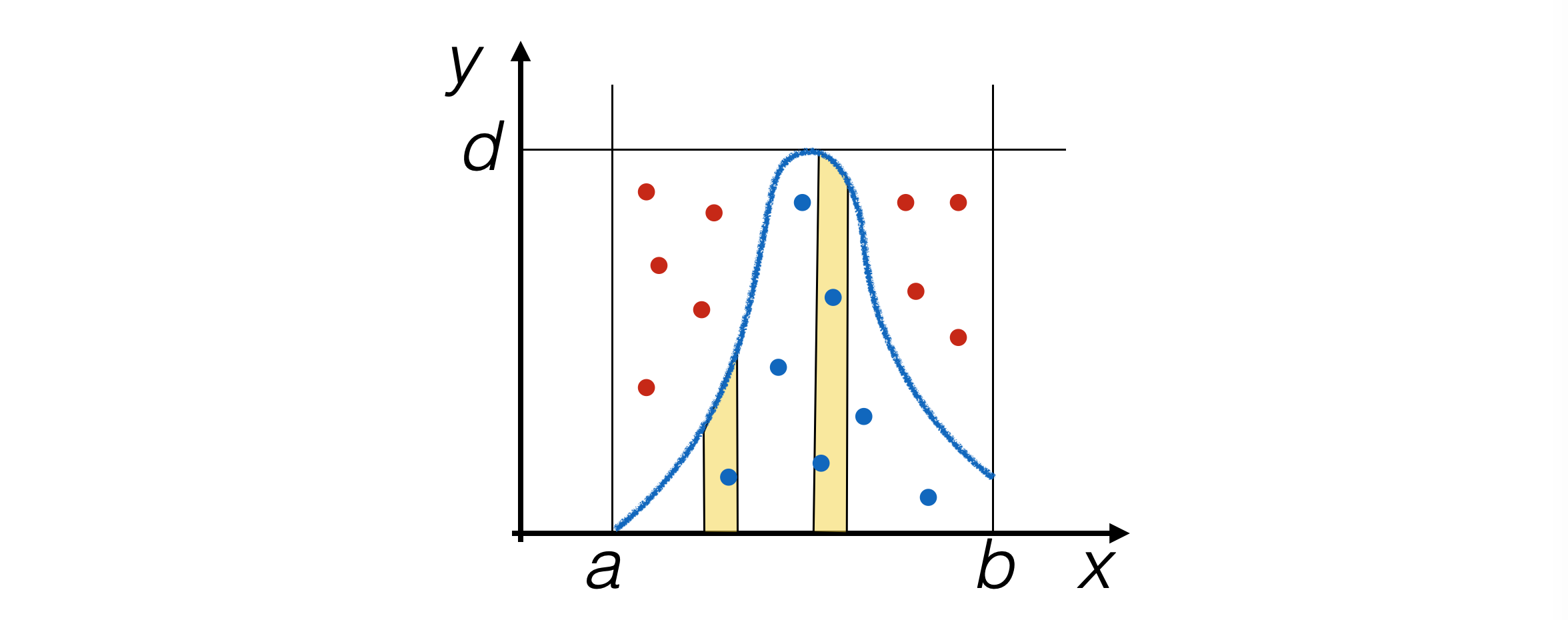
distribuzione_non_uniforme

  • popolare il piano con coppie di numeri pseudo-casuali x,y, ciascuno generato uniformemente con rand_range () e utilizzare x solo se y < f(x)

distribuzione_non_uniforme

linea

4.3.2 l’implementazione dell’algoritmo try-and-catch

  • per ripetere la generazione fino a che la condizione y < f(x) non è soddisfatta, si utilizza un ciclo:

    float rand_TAC (float f (float), float xMin, float xMax, float yMax)
  {
    double x = 0. ;
    double y = 0. ;
    do {
      x = rand_range (xMin, xMax) ;
      y = rand_range (0, yMax) ;
    } while (y > f (x)) ;
    return x ;
  }

  • la funzione rand_TAC ha bisogno di più argomenti rispetto a rand_range:

    • un limite superiore per l’asse verticale: yMax

    • la forma funzionale da usare come pdf: come vedete anche una funzione può essere passata come argomento ad un’altra funzione, descrivendone il prototipo

(esempio 4.3)

linea

4.3.3 vantaggi e svantaggi dell’algoritmo try-and-catch

vantaggi

  • nota la forma funzionale della pdf, l’algoritmo funziona

  • non è necessario che la pdf sia nota analiticamente, è sufficiente che si possa scrivere come funzione di C++

  • facilmente generalizzabile a N dimensioni

svantaggi

  • bisogna essere certi di conoscere il massimo (yMax) della funzione

  • ha bassa efficienza:

    • per ottenere un numero casuale, bisogna generarne di sicuro almeno due

    • spesso molti di più, perché molti punti sul piano vengono scartati

linea

4.4 altre distribuzioni di probabilità: la funzione inversa

  • sia x una variabile casuale con pdf f(x) continua

  • sia F(x) la distribuzione di probabilità cumulativa (cdf)

  • se F(x) è strettamente crescente allora la variabile y = F(x) ha distribuzione uniforme (si dimostra usando la regola per il cambio di variabile in una pdf)

  • generare eventi pseudo-casuali con distribuzione uniforme in y equivale a generare eventi pseudo-casuali lungo x con distribuzione f(x)

linea

4.4.1 l’algoritmo della funzione inversa

  • si calcolano analiticamente F(x) e la sua funzione inversa F -1(y)

funzione_inversa

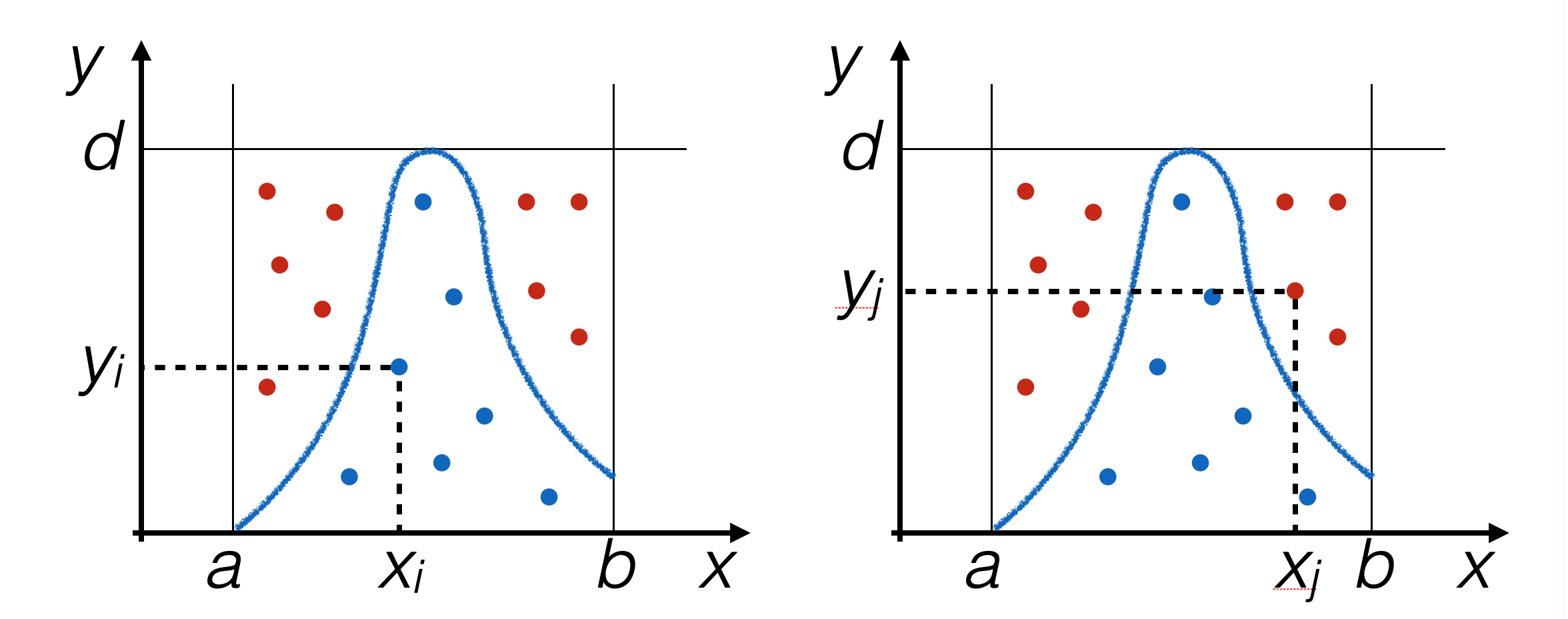
  • si generano numeri pseudo-casuali yi con distribuzione uniforme fra 0 ed 1 lungo l’asse y

  • per ogni evento generato, si calcola xi = F -1(yi) e si utilizza quel valore come numero casuale generato

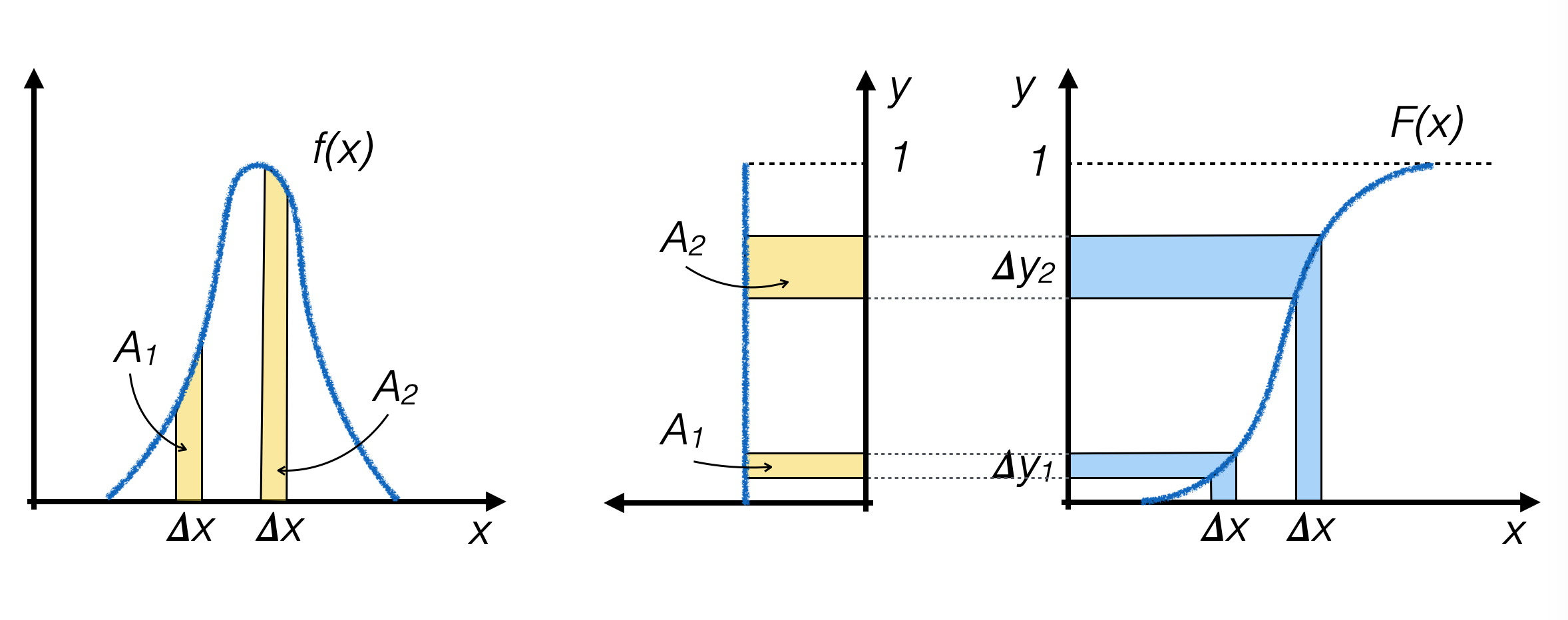
  • dove f(x) è più alta F(x) è più ripida, quindi il numero di numeri pseudo-casuali generati nei due intervalli Δy1 e Δy2 risulta proporzionale all’area sottesa dalla curva f(x) sopra i due intervalli con dimensione Δx, rispettivamente, che è l’obiettivo che si vuole ottenere.

linea

4.4.2 vantaggi e svantaggi dell’algoritmo della funzione inversa

vantaggi

  • è efficiente nella generazione dei numeri pseudo-casuali, perché ogni numero viene utilizzato

svantaggi

  • bisogna conoscere la forma analitica di f(x) ed F(x) e sapere invertire la funzione comulativa per ottenere F -1(y)

  • il calcolo di una funzione aggiunge tempo nella generazione degli eventi

linea

4.5 distribuzioni di probabilità Gaussiane: il teorema centrale del limite

  • Il teorema centrale del limite può essere utilizzato per generare distribuzioni di probabilità con forma Gaussiana

Siano date N variabili casuali xi indipendenti ed identicamente distribuite secondo una distribuzione di probabilità f(x) con media μ e varianza σ2 finite. Allora la variabile y = ⟨xi⟩ è distribuita, per N grande, come una Gaussiana con media μ e varianza σ2.

linea

4.5.1 l’implementazione dell’algoritmo

  • anche in questo caso, si parte da generatori di numeri pseudo-casuali noti: la distribuzione uniforme

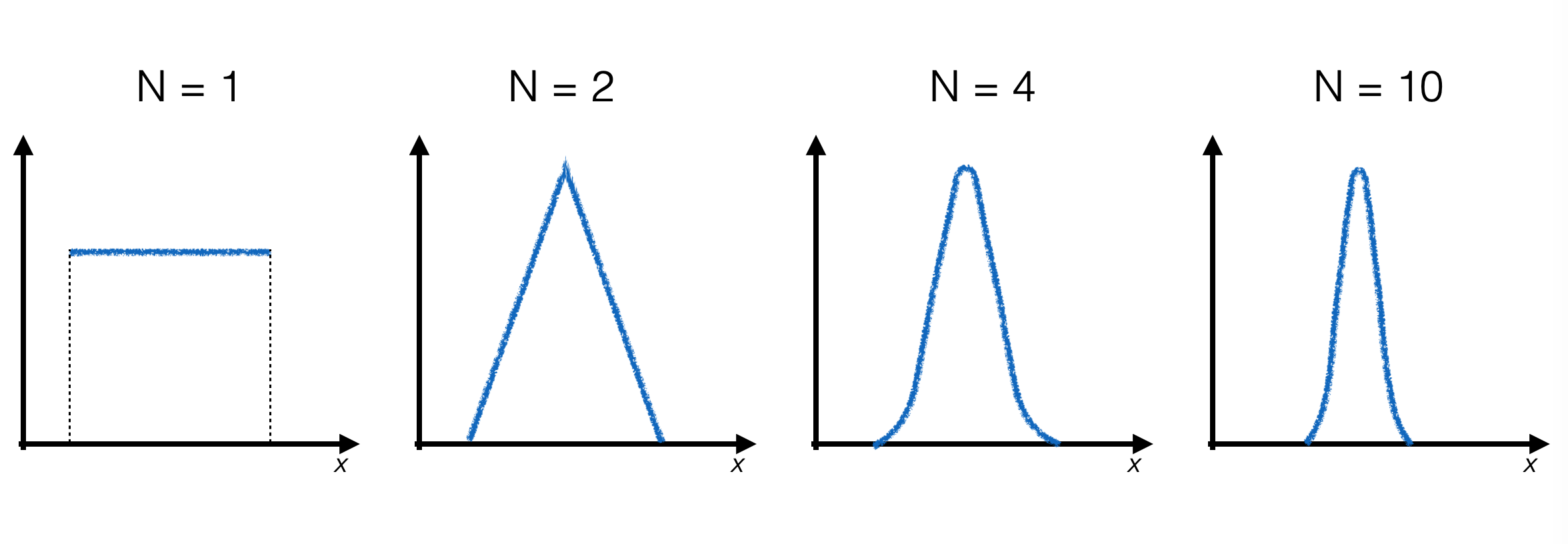
  • per produrre un singolo numero pseudo-casuale distribuito secondo una Gaussiana, è necessario generare N numeri pseudo-casuali secondo la distribuzione uniforme e calcolarne la media

  • al crescere di N la distribuzione finale si avvicina sempre più al limite Gaussiano:

funzione_inversa

(esempio 4.4)

linea

4.5.2 vantaggi e svantaggi dell’algoritmo per generazione di pdf con forma gaussiana

vantaggi

  • è basato su un ben noto teorema e permette di verificare (entro le approssimazioni numeriche di un calcolatore) che il teorema stesso funzioni

  • non è necessario descrivere analiticamente la forma funzionale della Gaussiana

svantaggi

  • per raggiungere una buona precisione, bisogna generare molti numeri pseudo-casuali uniformi per ottenerne uno distribuito secondo una distribuzione di Gauss

linea

4.6 ESEMPI

  • Gli esempi relativi alla lezione si trovano qui

4.7 ESERCIZI

  • Gli esercizi relativi alla lezione si trovano qui

previous

Soluzioni: Lezione 3

next

Esempi: Lezione 4