Contents

Lezione 7: La distribuzione di Poisson

Lezione 7: La distribuzione di Poisson

7.1 Rappresentazione di andamenti y vs x: i TGraph

  • gli istogrammi mostrano una singola variabile fisica

  • talvolta è utile visualizzare coppie di misure (x,y)

  • in ROOT la classe che si utilizza per farlo è il TGraph

linea

7.1.1 Definizione di un TGraph

  • come sempre, bisogna includere la libreria corrispondente:

    #include "TGraph.h"

  • ricordando di aggiungere le opzioni di ROOT al comando di compilazione:

    > c++ -o programma `root-config --cflags --glibs` programma.cpp

  • un oggetto di tipo TGraph si definisce semplicemente:

    TGraph g_sigma ;

    • l’oggetto è vuoto: non contiene alcuna variabile

    • esistono altri costruttori oltre a quello di default, che permettono di inizializzare un TGraph con un insieme di coppie di punti nulli oppure a partire da array già riempiti

linea

7.1.2 Riempimento di un TGraph

  • un TGraph viene riempito con il metodo TGraph::SetPoint (Int_t i, Double_t x, Double_t y), che prende in input:

    • l’indice del punto da riempire, che per il primo punto è 0

    • il valore della variabile x

    • il valore della variabile y

    g_sigma.SetPoint (g_sigma.GetN (), 11.5, 7.4) ;

    • in questo caso, come primo argomento si utilizza il metodo stesso TGraph::GetN (), perché per un TGraph che contiene N elementi l’indice dell’ultimo elemento salvato è N-1

  • si noti che ROOT ridefinisce le variabili numeriche del C++ (sostituendo int con Int_t e double con Double_t in questo caso), perché le variaibli definite internamente da ROOT hanno una dimensione in byte convenzionale

linea

7.1.3 Disegno di un TGraph

  • come nel caso di TH1F, un TGraph si disegna su un TCanvas:

    TCanvas c1 ("c1", "c1", 100, 100, 1000, 1000) ;
c1.SetLogx () ;
g_sigma.Draw ("ALP") ;
c1.Print ("sigmaTrend.png", "png") ;

    • le opzioni passate al metodo Draw richiedono di

      • tracciare gli assi (A)

      • congiungere i punti con una linea (L)

      • disegnare i marker ad ogni punto (P).

linea

7.1.4 Qualche opzione grafica

  • anche per un TGraph, si possono impostare diversi parametri grafici:

    g_sigma.SetMarkerStyle (20) ;
g_sigma.SetMarkerColor (kAzure - 1) ;
g_sigma.SetLineColor (kGray + 1) ;
g_sigma.SetMarkerSize (2) ;
g_sigma.GetHistogram ()->GetXaxis ()->SetTitle ("numero di eventi nel campione") ;
g_sigma.GetHistogram ()->GetYaxis ()->SetTitle ("deviazione standard") ;

    • il metodo TGraph::GetHistogram () restituisce il puntatore all’istogramma di servizio creato da ROOT per comporre graficamente il disegno

linea

7.2 I processi poissoniani

  • Un evento fisico che produce eventi casuali distribuiti nel tempo è di carattere Poissoniano se:

    • gli eventi sono indipendenti uno dall’altro

    • la probabilità che un evento accada non dipende dall’istante di misura

  • Se una sequenza di numeri casuali corrisponde ai tempi di un processo Poissoniano, allora è vero che:

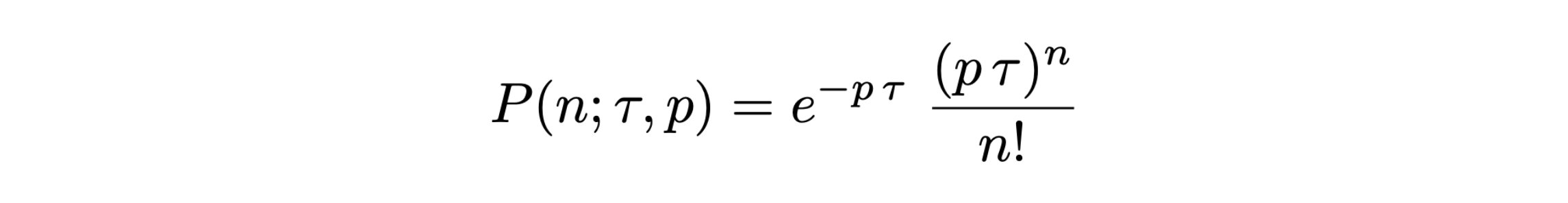
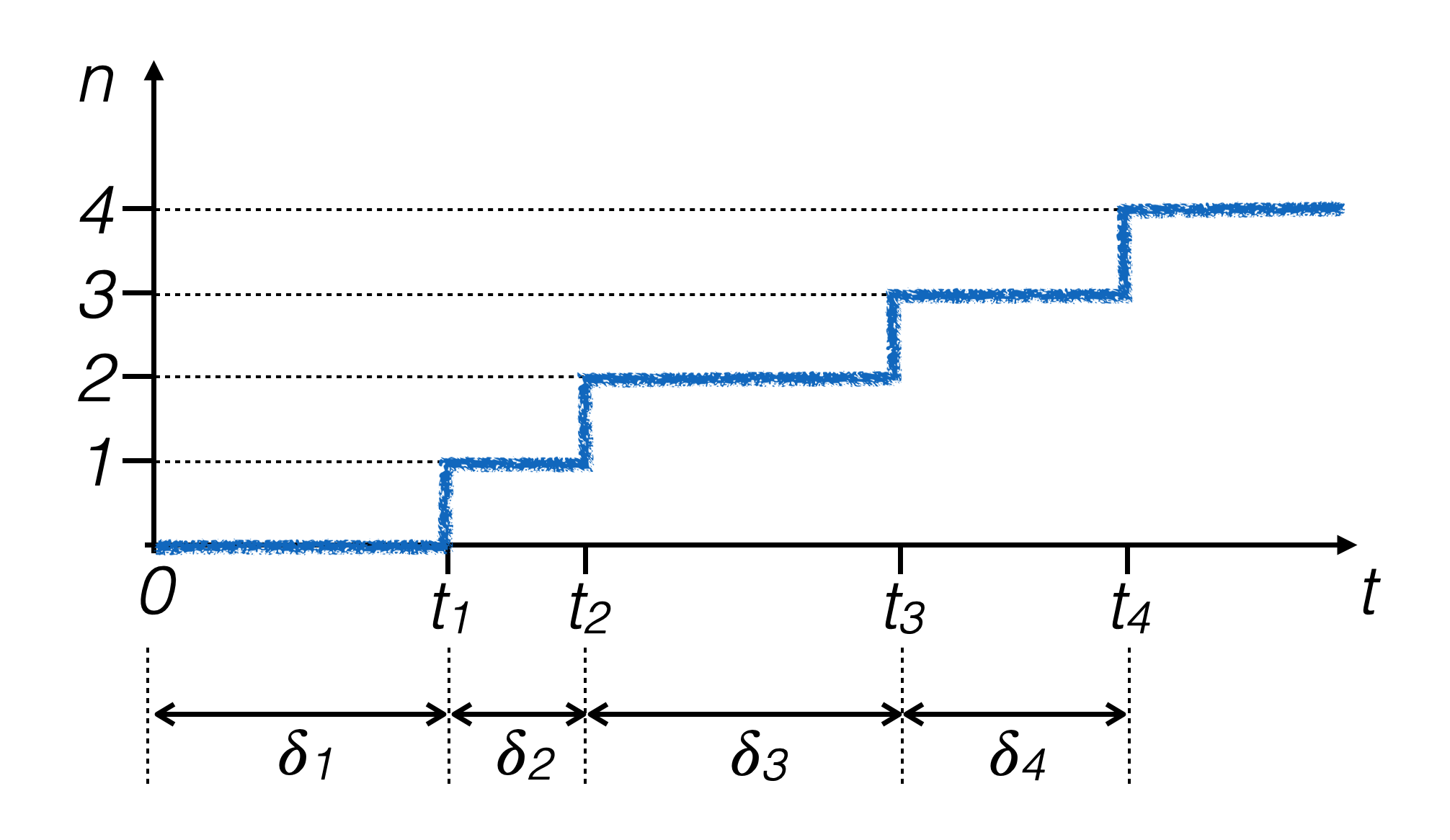
    • se la probabilità che l’evento accada dell’unità di tempo è p, il numero di eventi osservati in un intervallo di tempo τ segue la distribuzione di probabilità di Poisson: pois_exp

    • le differenze di tempo δi fra due eventi successivi seguono una distribuzione di densità di probabilità esponenziale pois_exp

linea

7.2.1 La generazione di eventi secondo una distribuzione di Poisson

  • per ottenere eventi pseudo-casuali distribuiti secondo una distribuzione di probabilità Poisson si può:

    • generare eventi secondo una distribuzione di densità di probabilità esponenziale con tempo caratteristico t0 unitario

    • contare quanti eventi caschino in un determinato intervallo \(\tau\) scelto con lunghezza \(\lambda\), se \(\lambda\) è la media di eventi attesa dalla distribuzione di Poisson

linea

7.3 Ripasso: la generazione di eventi secondo un distribuzione f(x) con la tecnica della funzione inversa

  • sia x una variabile casuale con pdf f(x) continua

  • sia F(x) la distribuzione di probabilità cumulativa (cdf)

  • se F(x) è strettamente crescente allora la variabile y = F(x) ha distribuzione uniforme (si dimostra usando la regola per il cambio di variabile in una pdf)

  • generare eventi pseudo-casuali con distribuzione uniforme in y equivale a generare eventi pseudo-casuali lungo x con distribuzione f(x)

linea

7.3.1 L’algoritmo della funzione inversa

  • si calcolano analiticamente F(x) e la sua funzione inversa F -1(y)

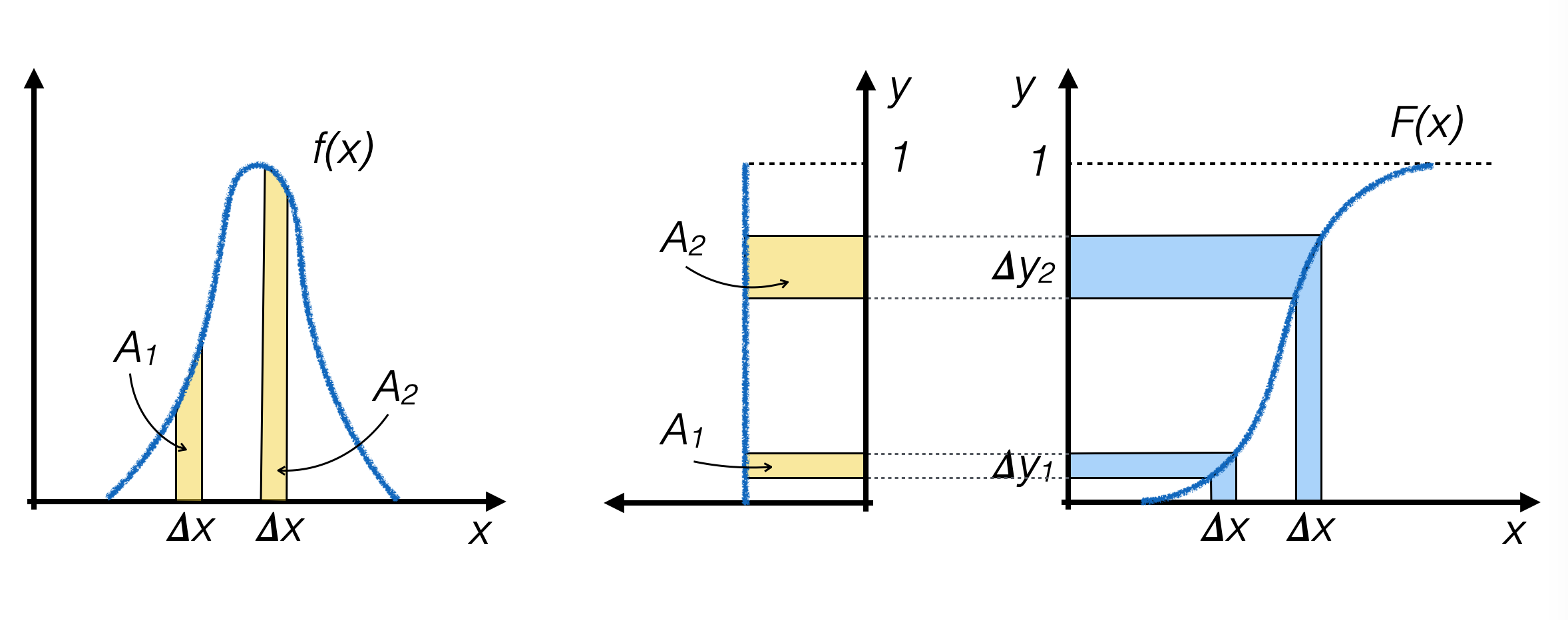
funzione_inversa

  • si generano numeri pseudo-casuali yi con distribuzione uniforme fra 0 ed 1 lungo l’asse y

  • per ogni evento generato, si calcola xi = F -1(yi) e si utilizza quel valore come numero casuale generato

  • dove f(x) è più alta F(x) è più ripida, quindi il numero di numeri pseudo-casuali generati nei due intervalli Δy1 e Δy2 risulta proporzionale all’area sottesa dalla curva f(x) sopra i due intervalli con dimensione Δx, rispettivamente, che è l’obiettivo che si vuole ottenere.

linea

7.3.2 Il caso esponenziale

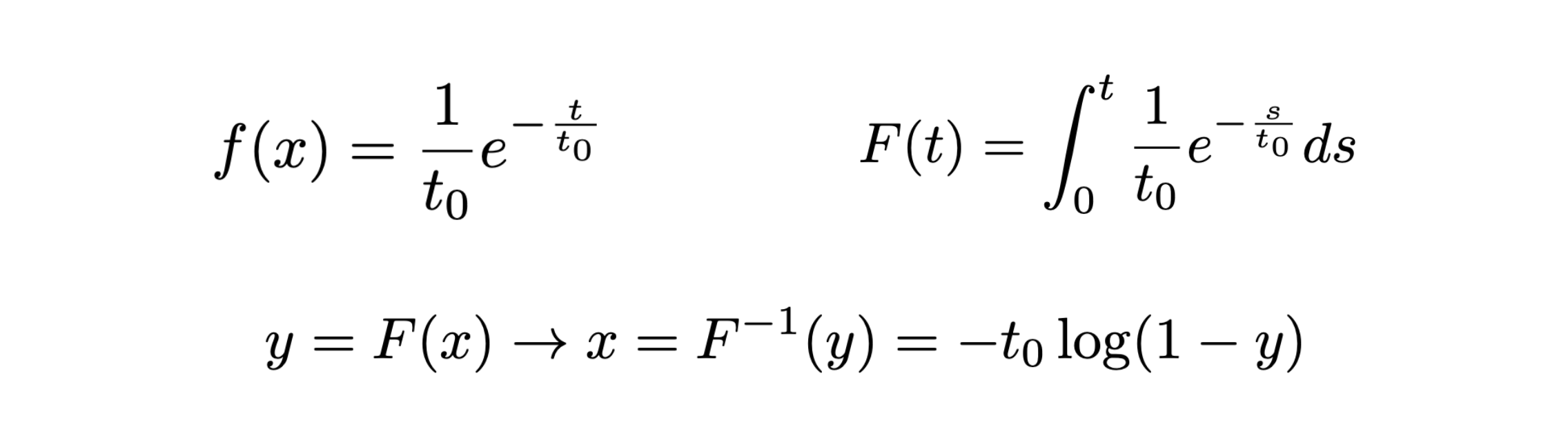
  • nel caso della distribuzione esponenziale, le richieste necessarie per l’applicazione del metodo sono soddisfatte, perché se ne conosce la primitiva e si può invertire: funzione_inversa_exp

    • in questo caso, la variabile y è un numero pseudo-casuale che segue una distribuzione di densità di probabilità uniforme fra 0 ed 1 (l’intervallo di valori che può assumere un esponenziale descrecente definito sull’asse positivo)

linea

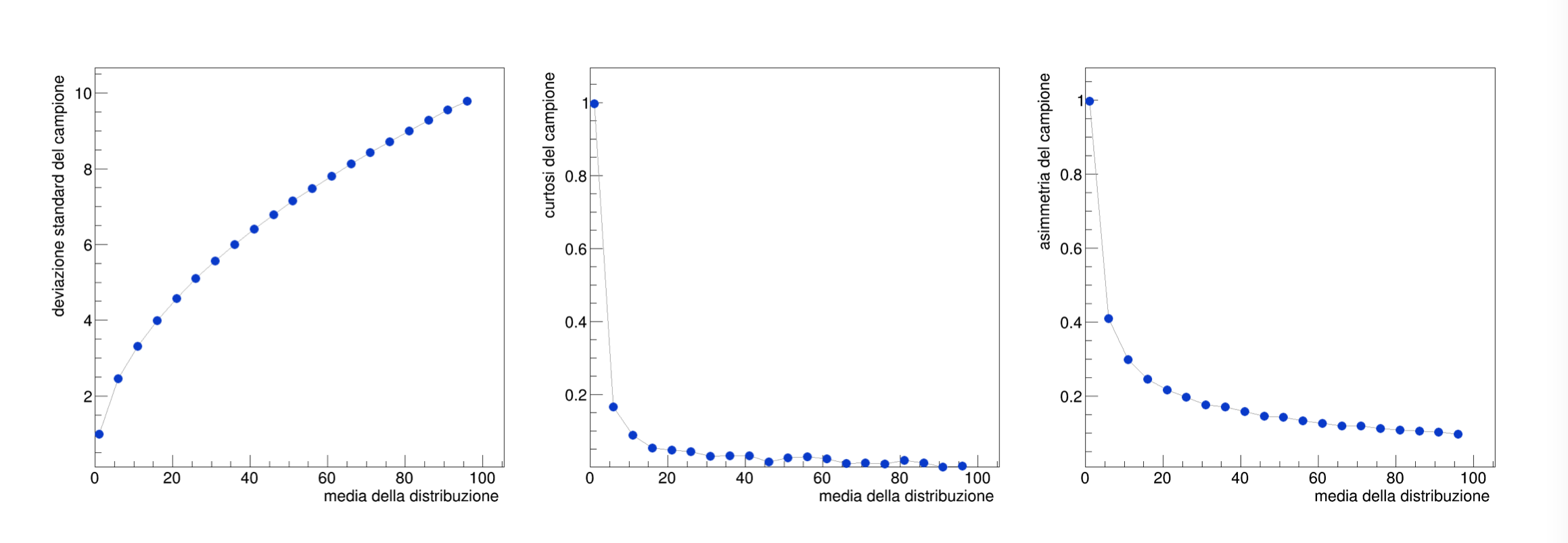
7.4 Le caratteristiche della distribuzione di Poisson

  • con gli strumenti descritti, si possono generare campioni di numeri pseudo-casuali di tipo Poissoniano e verificare le caratteristiche della loro distribuzione, attraverso lo studio dei momenti dei campioni generati, disegnati con TGraph di ROOT:

grafici

linea

7.5 ESERCIZI

  • Gli esercizi relativi alla lezione si trovano qui

previous

Soluzioni: Lezione 6

next

Esercizi per la lezione 7