9. The likelihood#

9.1. Programming with notebooks#

  • Notebooks are documents that contain rich text elements (paragraph, equations, figures, links, etc…) and computer code (e.g. python), and can show the output of the code integrated within the document.

  • They may be exploited in keeping in the same place the actual developed algorithms together with their description and results comments.

  • Python notebooks may be implemented locally, for example with the jupyter software, or remotely, for example with Google Colaboratory or with binder.

  • Notebooks may run source code written in them and load existing libraries.

9.2. jupyter notebooks#

  • In an environment where the jupyter program is installed, notebooks are accessible trough web browsers

  • The notebook user interface may be opened with the following shell command:

    jupyter notebook

  • This call opens a web browser window containing a list of the current folder and some commands among which that to create a new notebook

9.2.1. Creating a jupyter notebook#

  • After creating a new notebook, an empty page is generated, where single elements of the notebook may be added by clicking on the + button

  • Elements may be of two types:

    • Code, which shall be filled with actual python source code

    • Markdown, which shall be filled with rich text, formatted according to the Markdown syntax (this document is written using the markdown syntax)

9.2.2. Running a jupyter notebook#

  • Once a notebook as been created, it can be run.

  • The code sections are executed in sequence, as if they are part of a single source program, and the output of each element will appear just after it.

    Warning

    In a complex notebook, all elements need to be run sequentially from the beginning, to avoid mismatches between variable values across execution

  • The markdown sections will be compiled and graphically rendered according to the markdown syntax.

  • The computational engine that performs the actual calculations is called a kernel and in the python case is based on the ipython library

    Warning

    For each notebook a dedicated kernel is run, therefore it’s smart to avoid runnning several notebooks without shutting them down when not useful.

9.2.3. Accessing files on disk#

  • Files on disk may be accessed from a notebook, either to load existing libraries, or to write or read data files

  • The library shall be located in the same folder as the notebook, and used as in any other python source code

9.3. Google Colaboratory notebooks#

  • The Google suite gives access to a python notebook system, called Google Colaboratory

  • Each notebook may be accessed from the Google Colab starting page, or from Google Drive

  • The fundamental working principles of the notebooks are the same as the ones of jupyter

9.3.1. Using non-installed libraries in Google Colab#

  • Python libaries which are not installed in the Google operative system may be installed when needed, by using the pip installer within a notebook itself:

    # installing the iminuit library for use in a Google Colab notebook
!pip install iminuit
from iminuit import Minuit

9.3.2. Accessing Google Drive from a Google Colab notebook#

  • The disk which may be addressed from a Google Colab notebook is that provided by Google Drive

  • A Google Drive folder shall be mounted before being accessible:

from google.colab import drive
drive.mount ('/content/drive')

  • An official example notebook showing local file upload/download and integration with Google Drive may be found at this link

9.3.3. Notebooks pros and cons#

Important

Advantages

  • The code running, output and documentation are in the same place

  • The effects of code changes may be very quickly observed

Disadvantages

  • The overall call may not be seen at a glance with a text editor

  • The separate running of single cells may scramble the logic of the whole program

  • The running of the same notebook in different tabs generates random behaviours

9.4. The Likelihood#

  • All the information that characterizes an experiment, summarizing both the theoretical assumptions and the measurements taken, is encoded in the likelihood, defined as the product of the value of the probability density distribution calculated for each measurement taken (for independent identically-distributed random values xi):

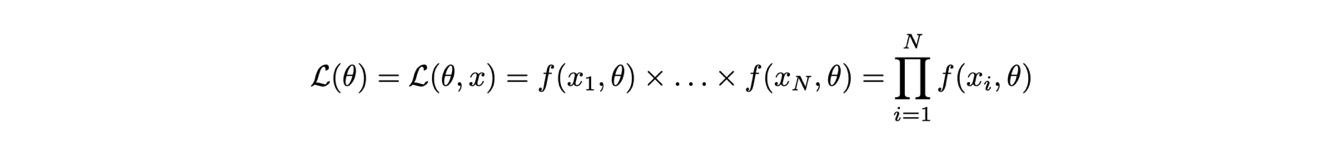
likelihood

  • The likelihood is a function of both the measurements and the parameters; however, usually only the dependence on the parameters is highlighted because with finite measurements, the data remain fixed.

9.4.1. A model describing the data#

  • A model is a probability distribution f or a law g to which measurements are expected to conform.

  • The measurement outcomes are variables with respect to which the model depends.

  • Any quantities on which the model depends, which are not measured, are referred to as parameters.

9.4.2. Probability Density Functions#

  • Given a set of real measurements xi defined on a set Ω that are independently and identically distributed, we know that they follow a given probability density distribution, generally denoted as f(x, θ).

  • This means that f(xi, θ) is the probability density for the measurement to occur at point xi within the definition set Ω.

  • The symbol θ indicates that the probability density function f depends on parameters other than x.

    • θ can also be a vector of parameters.

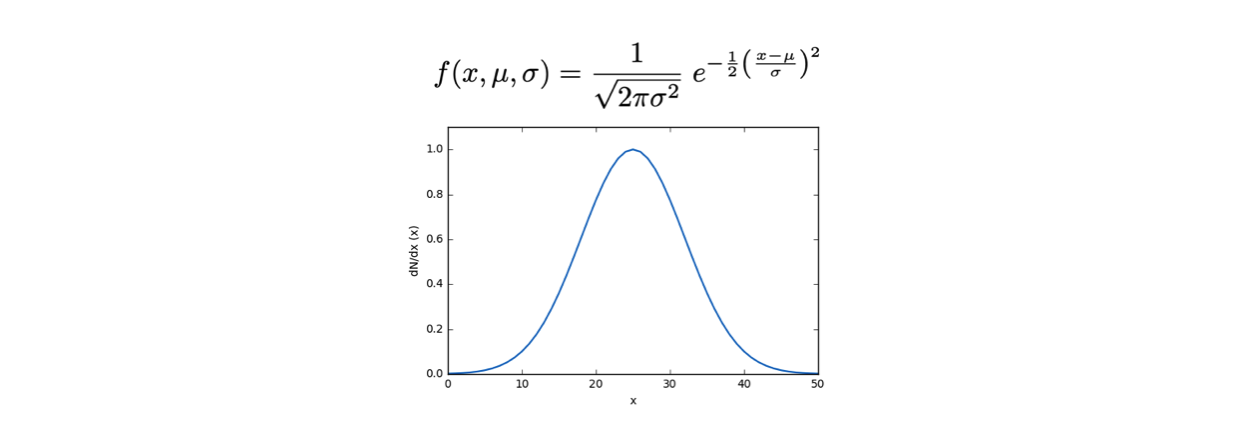
    • For example, a Gaussian distribution has two additional parameters, μ e σ: gaussian

9.5. The logarithm of the Likelihood#

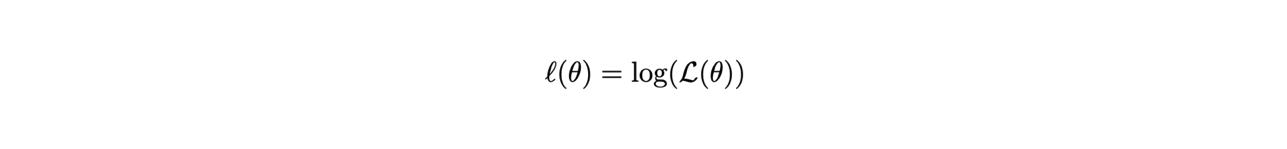
  • Often, for calculations and graphical representations, the logarithm of the likelihood function is used, denoted by a lowercase italic letter: loglikelihood

  • In fact, since the logarithm is a monotonically increasing function, the behavior of the likelihood and its logarithm are similar.

  • The logarithm of a product of terms is equal to the sum of the logarithms of the individual terms:

    \[\log(\mathcal{L}(\theta;\vec{x})) = \log\left(\prod_{i=1}^N f(x_i,\theta)\right) = \sum_{i=1}^N \log\left(f(x_i,\theta)\right)\]

  • The logarithm of a number is smaller than the number itself and varies over a smaller range compared to the variability of the number, therefore operations involving logarithms can be more numerically stable.

9.6. Building a Likelihood function#

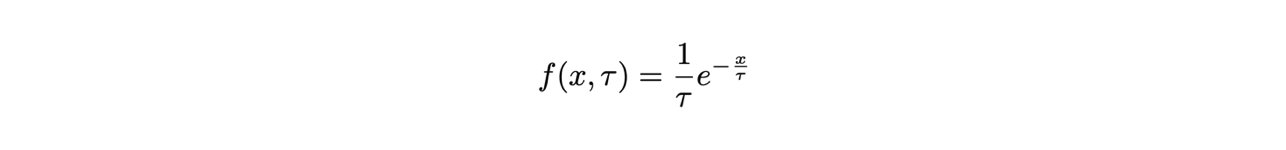
  • We will use the example of the exponential distribution, with the sole parameter τ as an additional argument of the likelihood: esponenziale

9.6.1. The Probability Density Function and the Likelihood function#

  • The first step in the study is the writing of the source code for the probability density function and the likelihood itself:

    def exp_pdf (x, tau) :      
    '''
    the exponential probability density function
    '''
    if tau == 0. : return 1.
    if x < 0. : return 0. 
    return exp (-1 * x / tau) / tau

    • the first if protects the program from infinity calculations

    • the second if guarantees that we have a Probability Density Function by limiting the integral to 1

  • the likelihood function will have as a input both the data and the parameter of interest:

    def loglikelihood (theta, pdf, sample) :
    '''
    the log-likelihood function calculated
    for a sample of independent variables idendically distributed 
    according to their pdf with parameter theta
    '''
    logL = 0.
    for x in sample:
      if (pdf (x, theta) > 0.) : logL = logL + log (pdf (x, theta))    
    return logL

    • in this case, the logarithm of the probability density function is calculated in each data point

Note

  • The exercises for the lecture may be found here