Data Visualisation with Python

3. Data Visualisation with Python#

3.1. Reading and writing text files with Python#

It is frequently useful to save data on text files and to be able to recover them for a later use, either to avoid inserting them one by one during a script execution, or to have them saved in a separate place with respect to the script source code.

3.1.1. Writing information on txt files#

The writing procedure may be done in the following way:
```
with open ('sample.txt', 'w') as output_file :
    for item in sample:
        # write each item on a new line
        output_file.write (str (item) + '\n')
```
- The sample variable is an existing collection of numbers
- the printout adds a carriage return symbol \n, so to ensure that the numbers are saved in different lines

3.1.2. Reading information from txt files#

The reading procedure may be done in the following way:
```
with open ('sample.txt') as input_file:
    sample = [float (x) for x in input_file.readlines()]
```
- The sample variabile gets created while reading the text file
- The readlines () function returns strings, which need to be converted into floats for them to be used as sample elements
Note

NumPy offers an alternative way to read data from text files and store them in arrays:
```
sample = np.loadtxt ('sample.txt')
```

3.2. Histograms#

Histograms are a graphical representation of the distribution of a sample of random numbers {x_i}_i=1,..,N usually called events.
An example of a sample of events is the set of measurements collected during an experiment.

3.2.1. Histogram Bins#

For a random variable of interest x, its interval of definition is divided into adjacent and disjoint sub-intervals delimited by {x_k}
- The k-th interval is bounded between x_k and x_k+1
- Usually, these intervals are called bins
An histogram is the collection of event counts that fall within each interval
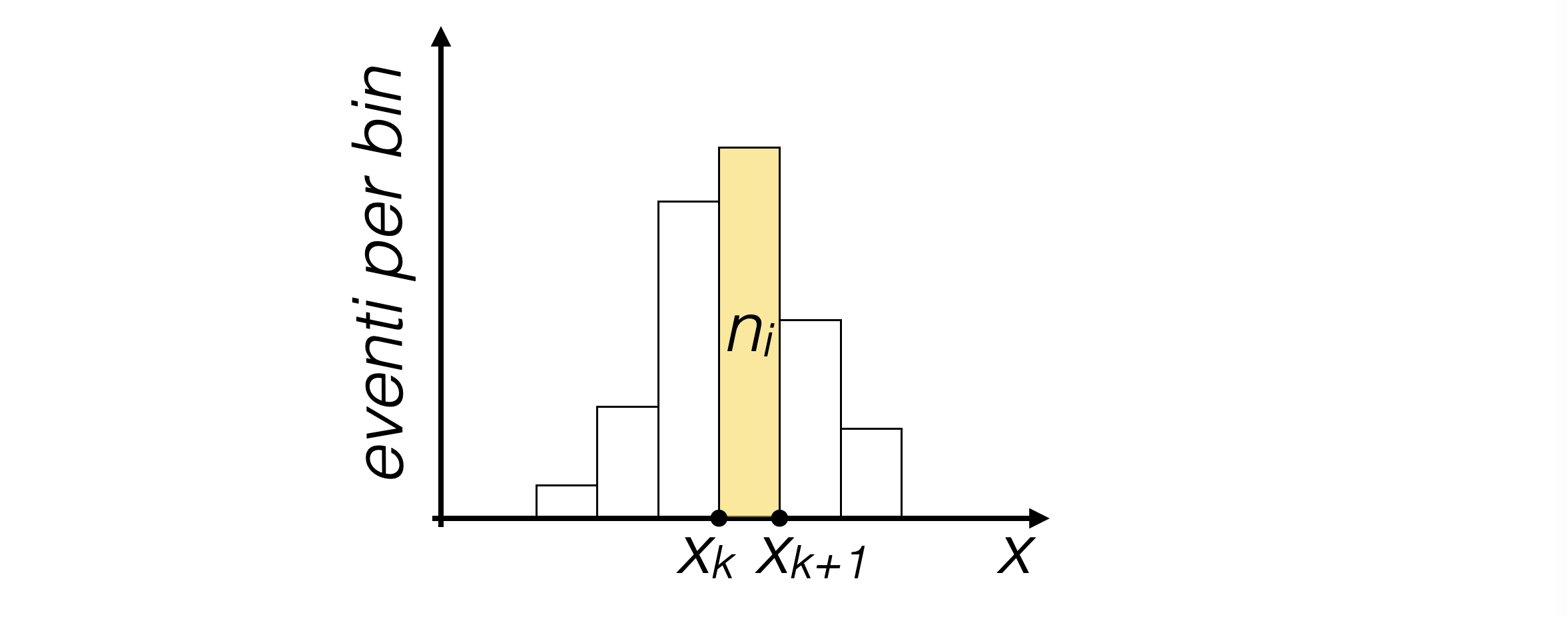
The visualization of a one-dimensional histogram typically shows:
- On the horizontal axis, the interval of definition of the variable x
- On the vertical axis, the counts corresponding to each bin
- Above each bin, a vertical bar as high as the counts in the bin

3.2.2. One-Dimensional Histograms and Probability Density Distributions#

As the bin size approaches infinitesimal, an histogram becomes a continuous function
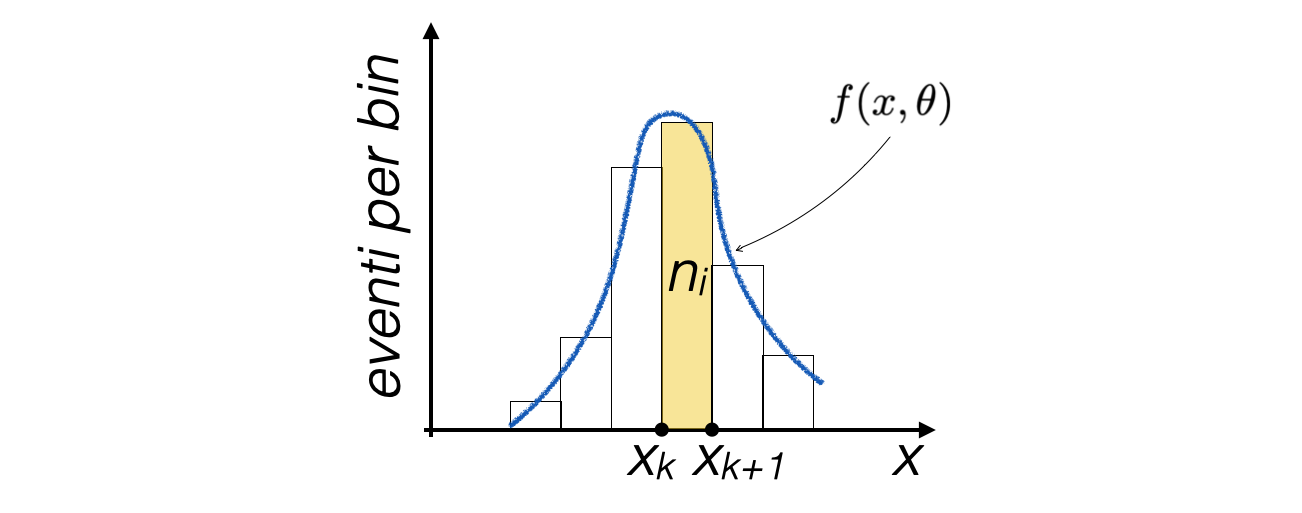
If the content of each bin is divided by the total number of events N, this function becomes normalized, thus an histogram approximates a probability density distribution

3.2.3. Histogram building and representation in `matplotlib`#

Given a sample of numbers, its visualisation in a histogram form may be obtained with the following instructions:
```
fig, ax = plt.subplots (nrows = 1, ncols = 1)
ax.hist (sample,
         color = 'orange',
        )
```
where the input sample is a collection of values
- The x axis range and its division into bins is automatically performed by the hist function

3.2.4. Histogram drawing options control#

Very frequenly – always in this course – one wants to have control over the x axis range and binning, for a proper statistical use of the histogram and for comparisons across histograms.

This may be achieved by explicitly defining the bin boundaries and providing them as input with the hist function:

bin_edges = np.linspace (xMin, xMax, N_bins)
print ('length of the bin_edges container:', len (bin_edges))
fig, ax = plt.subplots (nrows = 1, ncols = 1)
ax.hist (sample,
         bins = bin_edges,
         color = 'orange',
        )

3.2.5. The number of bins#

Depending on the sample size, the number of bins shall be adapted:
- on the one hand, with more events it may be increased, with very few events it has to remain small to gather at least some events per bin
- on the other hand, it’s of no use that the size of each bin is much smaller than the typical shape changes in the histogram

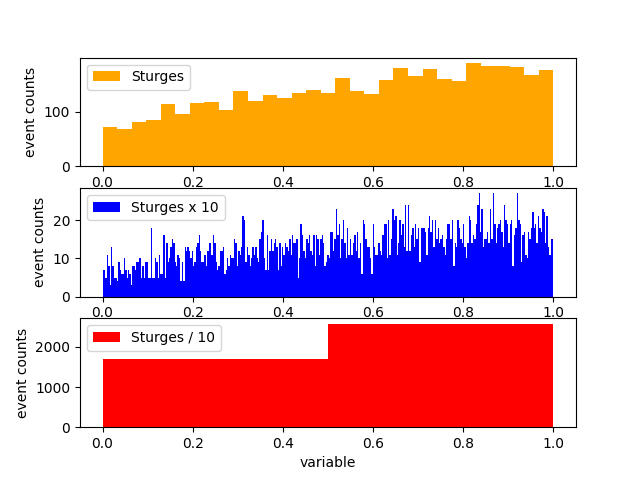
The choice of N_bins is therefore relevant for a proper representation: a recipe frequently used is the so-called Sturges’ rule:

import numpy as np
def sturges (N_events) :
     return int( np.ceil( 1 + np.log2(N_events) ) )

which may be used as follows in the drawing instructions:

N_bins = sturges (len (sample))
bin_edges = np.linspace (xMin, xMax, N_bins)

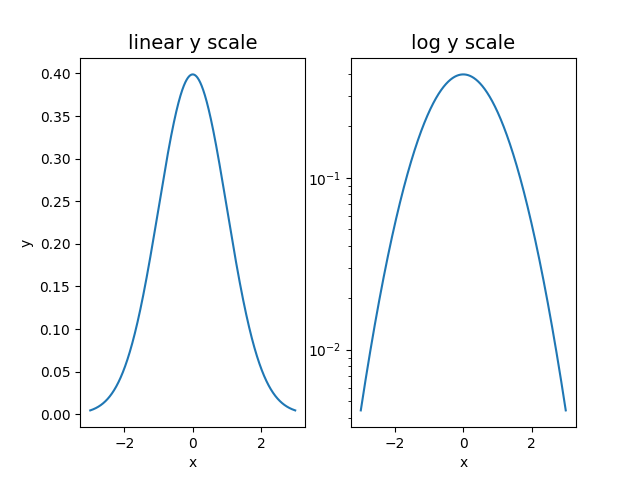
3.2.6. Logarithmic scales#

When the values in different bins change considerably, it can be convenient to visualize histograms on a logarithmic scale (along the horizontal or vertical axis), to improve the readability of the result
Being a different visualization of the same content, this operation is performed using a method of the axes object
```
ax.set_yscale ('log')
```
- Clearly, the zero of the logarithmic scale axis cannot appear in the images

3.3. Calculate and draw sample moments#

Given a sample, its moments may be calculated by replacing expectation values with sample averages, for example:

\[ E[x] = \int_{-\infty}^\infty x\:f(x)\:dx ~ \to ~ \sum^N_{i=1} x_i / N \]
The corresponding python script to implement this call is then:
```
return sum (sample) / len (sample)   
```
- the python function sum calculates the sum of the sample elements
- the python function len calculates its number of elements

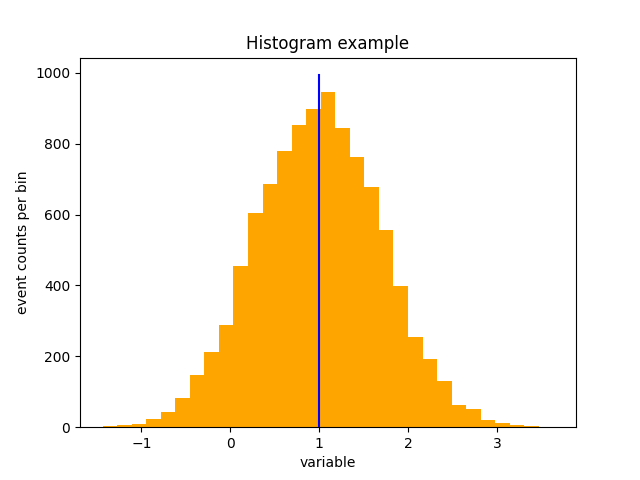
once the average is known, its drawing may be added on top of a histogram:

ax.hist (sample,
         bins = bin_edges,
         color = 'orange',
        )
vertical_limits = ax.get_ylim ()
ax.plot ([sample_mean, sample_mean], vertical_limits, color = 'blue')

to obtain the following visualisation mean_drawing

3.4. Data models#

Notable probability density function distributions exist in a pre-implemented form in the SciPy library, which provides algorithms and data structures for scientific computing.
The full list of available models may be found here
All continuous distributions take loc and scale as keyword parameters to adjust the location and scale of the distribution
- for the Gaussian distribution, the loc is the mean and the scale is the standard deviation
Note

Probability density functions f are usually written for a standardized variable, and the loc and scale parameters are used to generalise them, usually with the formula: $$ f(x, loc, scale) = \frac{1}{scale}f(\frac{x-loc}{scale}) $$

3.4.1. Using a continuous probability density function#

A pdf object needs to be imported from the SciPy library to be used, as for example for the Gaussian distribution:
```
from scipy.stats import norm
```

The actual values of the pdf may be accessed through the pdf function:

mean = 1.
sigma = 0.5
x = mean + sigma / 2.
print (norm.pdf (x, mean, sigma))

The values of the input parameters may be frozen once and for all:

norm_fix = norm (mean, sigma)
print (norm_fix.pdf (mean))

Note

For discrete probability density functions (e.g. Poisson, Binomial), for each single value on the domain axis a probability - not a density - is associated, and the corresponding function is called probability mass function, abbreviated as pmf.

3.4.2. The cumulative density function#

The function cdf gives access to the cumulative density function of the model, for example in the case of a Gaussian distribution:

print ('the value of the cumulative Gaussian distribution at its mean is: ' +
       str (norm.cdf (mean, mean, sigma))
       )

3.4.3. Distribution momenta#

The pdf objects provide functions for the calculation of their momenta:

ave, var, skew, kurt = norm_fix.stats (moments='mvsk')
print (ave, var, skew, kurt)

3.5. Function integration#

The SciPy library also contains a module dedicated to numerical integration of functions

3.5.1. Definite integral#

The function quad calculates definite integrals given the function and the integration range

from scipy.integrate import quad
# definition of a polinomial function
def polin(x): return x**2 + x + 1

area = quad (polin, 0., 4.)
print ('area = ', area[0])
print ('absolute error estimate = ', area[1])

The quad function returns both the integral value and an estimate of the absolute error on the integral

3.5.2. Integration over infinite ranges#

The quad function works with infinity extremes, which can be expressed thanks to the numpy object np.inf:
```
def expon (x): return exp (-1 * x)

area = quad (expon, 0, np.inf)
```